Astfel, PMF este o măsură de probabilitate care ne dă probabilitățile de valori posibile pentru o variabilă aleatoare. În timp ce notația de mai sus este notația standard pentru PMF de $X$, ar putea părea confuz la început. Indicele $X$ aici indică faptul că acesta este PMF al variabilei aleatorii $X$. Astfel, de exemplu, $P_X(1)$ arată probabilitatea ca $X=1$., Pentru a înțelege mai bine toate conceptele de mai sus, Să analizăm câteva exemple.deși PMF este de obicei definit pentru valorile din interval, uneori este convenabil să se extindă PMF de $X$ la toate numerele reale. Dacă $x \nu R_X$, putem scrie pur și simplu $P_X(x)=P(X=x)=0$. Astfel, în general, putem scrie \begin{equation} \nonumber P_X(x) = \left\{ \begin{array}{l} P(X=x) & \quad \text{dacă $x$ este în } R_X\\ 0 & \quad \text{în caz contrar} \end{array} \right. \ end{equation}

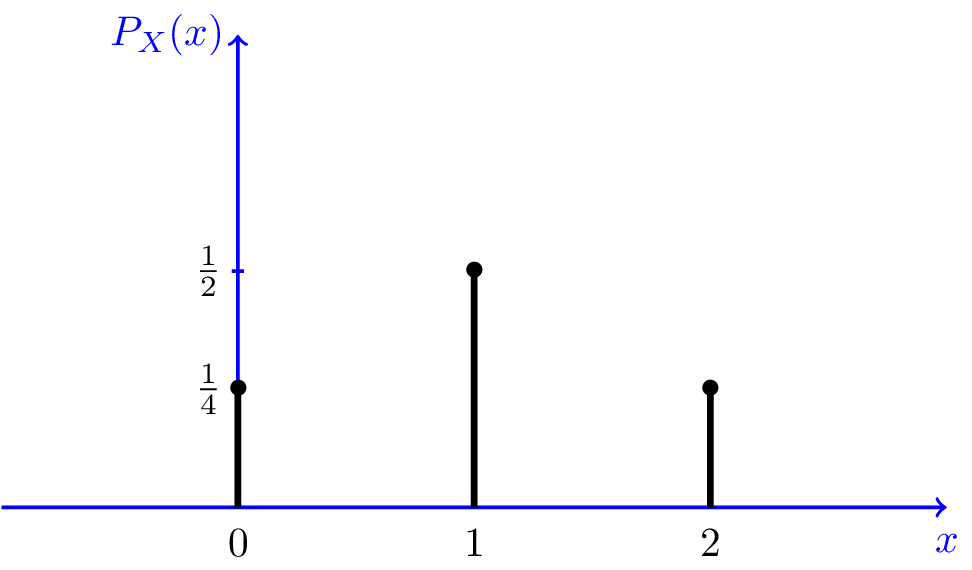
pentru a vizualiza mai bine PMF, o putem trasa. Figura 3.,1 arată PMF a variabilei aleatoare de mai sus $X$. După cum vedem, variabila aleatorie poate lua trei valori posibile $0,1$ și $2$. Cifra indică, de asemenea, în mod clar că evenimentul $X=1$ este de două ori mai probabil decât celelalte două valori posibile. Cifra poate fi interpretată în felul următor: dacă repetăm experimentul aleatoriu (aruncând o monedă de două ori) de un număr mare de ori, atunci aproximativ jumătate din ori observăm $X=1$, aproximativ un sfert de ori observăm $X=0$ și aproximativ un sfert de ori observăm $X=2$.

pentru variabilele aleatoare discrete, PMF este, de asemenea, numit distribuția probabilității. Astfel, atunci când li se cere să găsească distribuția de probabilitate a unei variabile aleatoare discrete $X$, putem face acest lucru găsind PMF-ul său. Funcția de distribuție a frazelor este de obicei rezervată exclusiv funcției de distribuție cumulativă CDF (așa cum este definită mai târziu în carte). Distribuția cuvântului, pe de altă parte, în această carte este folosită într-un sens mai larg și se poate referi la PMF, funcția de densitate de probabilitate (PDF) sau CDF.,am o monedă neloială pentru care $P (H)=P$, unde $0

ia în considerare o variabilă aleatoare discretă $X$ cu interval$(X) = r_x$. Rețineți că, prin definiție, PMF este o măsură de probabilitate, deci satisface toate proprietățile unei măsuri de probabilitate. În special, avem

• $0\leq P_X(x) \leq 1$ pentru $x$, iar
• $\sum_{x \în R_X} P_X(x)=1$.

rețineți, de Asemenea, că, pentru orice set $O \subset R_X$, putem găsi probabilitatea ca $X \in O$ folosind PMF$$P(X \a)=\sum_{x \în} P_X(x).,$$

Exemplu

Pentru variabila aleatoare Y $$ în Exemplul 3.4,

1. Verificați că $\sum_{y \in R_Y} P_Y(y)=1$.
2. dacă $p=\frac{1}{2}$, Găsiți $P (2 \ leq Y