Partea I
Dezvoltarea de Calcul
Istoria are un mod de focalizare de credit pentru orice invenție sau descoperire pe una sau două persoane într-un timp și loc. Adevărul nu este la fel de curat. Când dăm impresia că Newton și Leibniz au creat calcule din pânză întreagă, le facem elevilor noștri un deserviciu. Newton și Leibniz erau strălucitori, dar nici măcar nu erau capabili să inventeze sau să descopere calculul.,corpul de matematică pe care îl cunoaștem ca calcul s-a dezvoltat de-a lungul multor secole în multe părți diferite ale lumii, nu doar în Europa de Vest, ci și în Grecia antică, Orientul Mijlociu, India, China și Japonia. Newton și Leibniz a atras pe un corp vast de cunoștințe despre subiecte atât în calculul diferențial și integral. Subiectul va continua să evolueze și să se dezvolte mult timp după moartea lor. Ceea ce marchează Newton și Leibniz este că ei au fost primii care au stat, au înțeles și au folosit eficient Teorema fundamentală a calculului., Nu există doi oameni s-au mutat înțelegerea noastră de calcul la fel de departe sau la fel de repede. Dar problemele pe care le studiem în calcul—zone și volume, rate conexe, poziție/viteză/accelerație, serii infinite, ecuații diferențiale—au fost rezolvate înainte de nașterea lui Newton sau Leibniz.a fost nevoie de aproximativ 1.250 de ani pentru a trece de la integrala unui cuadratic la cea a unui polinom de gradul patru. Dar conștientizarea acestei lupte poate fi un memento util pentru noi. Rezultatele grandioase care rezolvă atât de multe probleme atât de ușor (integrarea unui polinom fiind un prim exemplu) ascund o lungă luptă conceptuală., Când sărim prea repede la algoritmul magic și nu reușim să recunoaștem efortul care a intrat în crearea sa, riscăm să tragem studenții noștri dincolo de acea înțelegere conceptuală.acest articol explorează istoria calculului înainte de Newton și Leibniz: oamenii, problemele și locurile care fac parte din povestea bogată a calculului.Abu Ali Al-Hasan ibn al-Haytham (cunoscut și prin forma latinizată a numelui său: Alhazen) a fost unul dintre marii matematicieni arabi. S-a născut în Basra, Persia, acum în sud-estul Irakului., Cândva după 996, s-a mutat la Cairo, Egipt, unde a devenit asociat cu Universitatea din Al-Azhar, fondată în 970. A scris peste 90 de cărți și este cel mai renumit pentru munca sa în astronomie și optică. Interesul său pentru matematică a variat peste algebră, geometrie și teoria numerelor. Mă concentrez asupra lui pentru că este prima persoană pe care o cunosc care a integrat un polinom de gradul patru.desigur ,el nu a exprimat-o în acest fel. În jurul anului 250 î. HR., Arhimede a scris Pe Conoids și Sferoide, o carte care, printre alte lucruri, a demonstrat cum de a găsi volumul unui parabaloid, solid de revoluție pe care le obține atunci când rotiți unei parabole în jurul axei sale (a se vedea Figura 1)., În special, dacă a și b sunt constantele pozitive și vom lua regiune delimitată mai sus, prin graficul de parabola de mai jos de axa x, și la dreapta prin x = o (a se vedea Figura 2), și rotiți această regiune în jurul axei x, vom obține solid de revoluție a cărui volum este
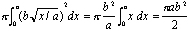
cu alte cuvinte, volumul este exact jumătate din cilindru că veți obține dacă rotiți dreptunghi de lungime a și înălțime b în jurul axei x.
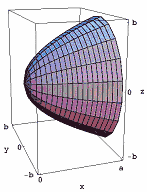
Figura 1: parabaloid.

Figura 1: parabaloid.,
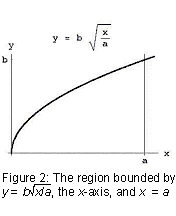

Cea mai dificilă parte a acestui calcul, ceva care a luat un matematician a lui Arhimede statura de a realiza, este că problema de a găsi volumul unui parabaloid poate fi redus la acela de a găsi zona de sub o linie dreaptă (integrală din x de la 0 la a).,
În lumea Arabă din secolul al zecelea, Arhimede Pe Conoids și Sferoide a fost necunoscut, dar Thabit ibn ai coranului de sud, Turcia și Abu Sahl al-Kuhi de nord, Iranul a descoperit propriile lor dovezi de volumul de parabaloid. Ibn al-Haytham le-a citit lucrarea și și-a pus întrebarea: Ce se întâmplă dacă rotim această regiune în jurul liniei x = a în loc de axa x?
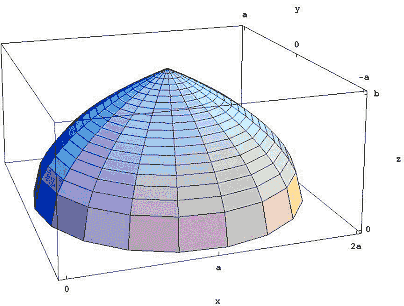
Figura 3: rotirea regiunii în jurul liniei x = a.
rezultatul este cupola foarte islamică prezentată în Figura 3., Ibn al-Haytham a arătat că volumul său este de 8/15ths din volumul cilindrului care o ai atunci când rotiți dreptunghi de lungime a și înălțime b în jurul valorii x = a. În notația modernă de calcul, calculul acest volum devine
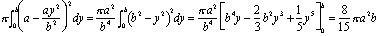
Dar ibn al-Haytham a trăit aproape 700 de ani înainte de formule pentru integrale-ar fi cunoscut. El a găsit volumul prin stivuirea discurilor. Dacă tăiem cupola în discuri nv, fiecare cu grosimea b / n, atunci discul i din partea de jos are raza a – ai2/n2 și volumul (b/n) p (a – ai2/n2)2 (vezi Figura 4)., Volumul total al acestei stive de discuri este
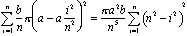
tot ce rămâne este să găsești o formulă—în termeni de n—pentru însumare. Apoi vedem ce se întâmplă pe măsură ce n se apropie de infinit. Ne vom extinde sumand și scoate constant competențele n:
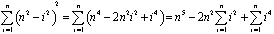
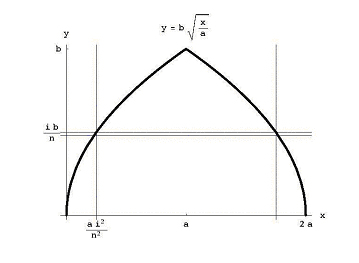
Figura 4: orizontală felie peste cupola.pentru ibn al-Haytham în ceea ce privește matematicienii din Orientul Mijlociu, Asia de Sud și Asia de Est, problema calculării zonelor și volumelor s-a redus la problema găsirii sumelor de puteri ale numerelor întregi consecutive., Ibn al-Haytham a fost unul dintre numeroșii matematicieni din multe locuri diferite care au reușit să rezolve această problemă. El a arătat că:
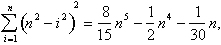
volumul de cupola este:
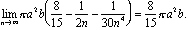
Cum de a găsi această concluzie? Această poveste se întinde pe două mii de ani și pe trei continente.
Partea a II-a
Arhimede și Sume de Pătrate
Nici o descriere de calcul înainte de Newton și Leibniz ar putea fi completă fără un cont de contribuțiile lui Arhimede, grecii Sicilieni care s-a născut în jurul 287 î. hr. și a murit în 212 B. C., în timpul asediului Roman al Siracuzei. Vom analiza una dintre numeroasele probleme de calcul pe care le-a studiat.este obișnuit să-l credităm pe Arhimede cu cele mai vechi agitări ale calculului integral. Printre problemele abordate și rezolvate sunt găsirea zone în parabole și în interiorul spirale, și de a găsi volumul sferei, sferice segmente, și parabaloid (solid de revoluție obținute de tip revolving unei parabole în jurul axei sale). El a arătat, de asemenea, cum să calculeze panta unei linii tangente la o spirală, prima licărire a calculului diferențial.,
frumusețea calculului așa cum știm acum că vine din simplitatea sa. Teorema fundamentală a calculului ne permite să rezolvăm probleme foarte dificile prin aplicarea unor proceduri simple de calcul care sunt justificate de Teorema fundamentală. Arhimede nu avea aceste lucruri, așa că a trebuit să se bazeze pe principii de bază și, cu multă ingeniozitate, să vină cu soluții inteligente.Arhimede a găsit volume ale parabaloidului și ale altor solide folosind un argument de echilibrare în care a comparat momentele diferitelor solide., El a calculat aria de sub o parabolă nu prin metoda obișnuită de aproximare a acesteia printr-o sumă de pătrate, ci folosind o observație geometrică care i-a permis să reducă problema la găsirea sumei unei serii geometrice. Aceasta este una dintre o serie de utilizări importante ale seriilor geometrice care au contribuit la dezvoltarea calculului.
problema pe care vreau să mă concentrez este aceea de a găsi zona din interiorul unei spirale. În coordonate polare, spirala arhimedeană (vezi Figura 5) este r = kq pentru o anumită constantă k., În coordonate dreptunghiulare, este curba cu ecuații parametrice: x (t) = k · t · cos t, y(t)=k · t · sin t, t > = 0.
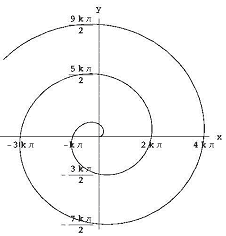
Figura 5: spirala lui arhimede
Arhimede angajat ceea ce a ajuns să fie cunoscut sub numele de „metoda de epuizare.”Ideea este de a aproxima zona folosind piese din ce în ce mai mici a căror suprafață poate fi găsită exact și apoi pentru a dovedi că o anumită valoare este răspunsul arătând că orice mai mic este prea mic și orice mai mare este prea mare.,
Arhimede atributele această metodă pentru a Eudoxus din Cnid (408-355 î. hr.) care a demonstrat că volumul de orice formă de piramidă sau de con este o treime din aria bazei înmulțită cu înălțimea. În timp ce Eudoxus găsit prima dovadă, acest rezultat este chiar mai vechi: s-a constatat de către Democrit (c. 465-375 B. C.). Formula pentru volumul piramidei a fost descoperit, de asemenea, în India antică, și ne-am înregistrat în cartea Chineză Chiu Chang Suan Ching (Nouă Capitole pe Matematice de Artă), care poate au fost scrise cât mai devreme 150 B. C.,chiar înainte ca cineva să poată dovedi această formulă, constatând că este necesară gândirea piramidei ca fiind formată din felii subțiri, din care trei seturi ar putea fi reconfigurate pentru a face un bloc dreptunghiular. Mai târziu, în acest articol vom vedea cum această geometrie tridimensională mentală l-a condus pe Arhimede la formula de care avea nevoie pentru a găsi zona spiralei.
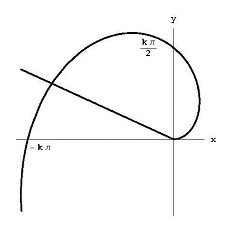
Figura 6: aria delimitată de spirala arhimedeană și raza q = q1.,pentru a găsi zona delimitată de spirală și raza q = q1, așa cum se arată în Figura 6, împărțim unghiul dintre raze în n unghiuri mici de dimensiune q1/n. dacă ne uităm la a i – a bucată de unghi, distanța spiralei de la origine crește de la k(i – 1) q1/n la ki q1 / n. aceasta înseamnă că zona noastră se află în interiorul sectorului razei ki q 1/ n. zona noastră include în întregime sectorul unghiului.cercul razei k(i-1) Q1/ n.,
unghiul t1/ n reprezintă t1 / 2 p n de un cerc complet, astfel încât zona de acest sector este undeva între
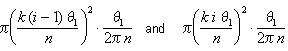
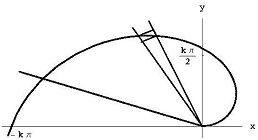
Figura 7: sectorul între q = k(i – 1)t1/n și q=ki t1/n
Când ne-am simplifica aceste limite, vom vedea că zona de al i-lea segment se află între k2q 13 (i – 1)2/2n3 și k2q13 i2 /2n3. Suprafața totală se află între
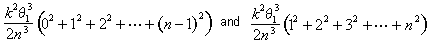
În acest punct, Arhimede a derivat o succintă formula pentru suma primelor n – 1 pătrate:
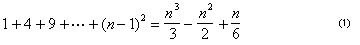 .,
.,
zona De sub spirala se află undeva între
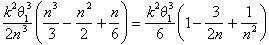
și
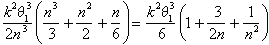
Ca Arhimede acum argumentat, singurul număr care se află între aceste limite pentru toate valorile lui n este k2 q13 /6.
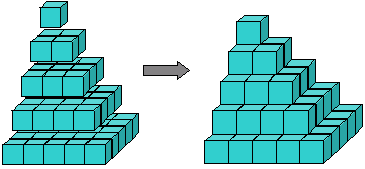
Figura 8: piramida de pătrate
Formula pentru Suma de Pătrate
formula pentru suma de pătrate poate nu am fost noi la Arhimede, și există dovezi că acesta ar fi fost descoperit cam în același timp în India. Știm că a fost redescoperit de multe ori., Primele dovezi, inclusiv dovada lui Arhimede, sunt toate geometrice.putem vizualiza suma pătratelor ca o piramidă construită din cuburi (figura 8). Arhimede a arătat cum să ia trei dintre aceste piramide împreună cu un strat triunghiular de blocuri reprezentând 1+2···+ (n – 1) și montați – le împreună pentru a obține un bloc de cuburi n x n x (n-1). Cu alte cuvinte, el a arătat că
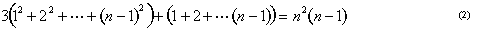 .
.
formula 1+2+···+ (n – 1)=N (n – 1)/2 este adesea atribuită lui Gauss. Povestea este că a descoperit – o când profesorul său ia ordonat să adauge numerele întregi de la 1 la 100., De fapt, este o formulă veche. Poate fi găsit, de exemplu, în India într-un manuscris Jain din 300 î.HR.: ar fi făcut parte din propria instrucțiune matematică a lui Arhimede. Are o dovadă geometrică foarte simplă, așa cum se arată în Figura 9.
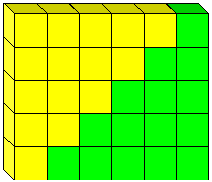
Figura 9: dovada că 2 = n(n-1)
Noi încă mai trebuie să dovedească ecuația (2), dar odată ce știm că este adevărat, putem combina-l cu formula pentru suma primelor n – 1 numere întregi pentru a obține
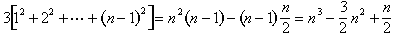
impartim ambele parti cu 3, și vom obține ecuația (1).,
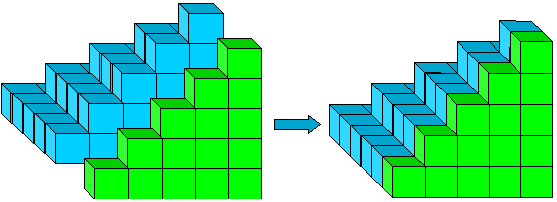
Figura 10: 12+22+···+(n – 1)2 +1+2+···+(n – 1).
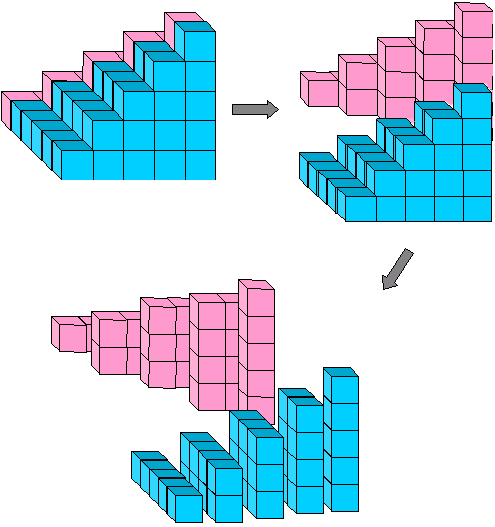
Figura 11: 1· 2 + 2·3 + 3·4 +···+ (n-1)n = 2
ecuație algebrică care corespunde această imagine este
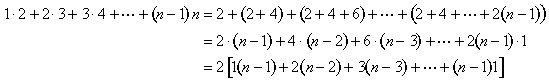
Aceste piese se potrivesc în jurul verde piramida din Figura 8, astfel încât o mai piramidă inversată completeaza n x n x (n – 1) bloc (Figura 12):
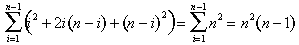
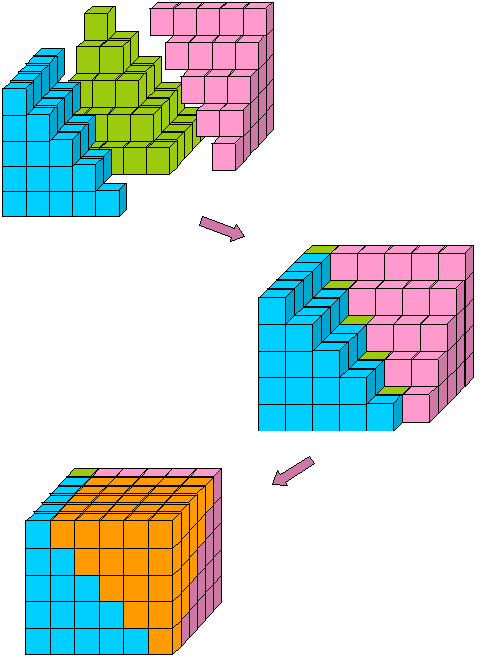
Figura 12: n x n x (n – 1) bloc asamblat din trei sume de pătrate și o sumă de numere întregi.,s-ar putea să credeți că, văzând cât de utilă este formula suma pătratelor, Arhimede ar fi găsit atunci formula pentru suma cuburilor. A durat mai mult de o mie de ani înainte ca cineva s-o facă. Problema este că sumele de pătrate sunt ușor de văzut geometric. Sumele de cuburi pot fi vizualizate, dar obiectul pe care doriți să le puneți împreună pentru a forma este patru-dimensional. Dar, după cum vom vedea în partea a III-a, până când Europa era în Evul Mediu, matematicienii din Orientul Mijlociu, India și China au făcut-o cu toții.,
partea a III-a
sume de puteri
în primele două părți ale acestui articol, am văzut cum Arhimede și ibn al-Haytham au folosit formule pentru sume de puteri pentru a evalua zonele și volumele. Începând cu secolul al XI-lea, matematicienii arabi, chinezi și indieni au început să descopere tehnici care să le permită să găsească zona sub orice polinom. Dar înainte ca cineva să poată descoperi astfel de formule, trebuiau să inventeze polinoame. Polinoamele pătratice și cubice au existat de peste o mie de ani, dar exprimate ca zone și volume., Nici măcar nu era clar ce ar însemna o a patra putere. Polinoamele de grad superior au apărut aproape simultan în jurul anului 1000 în Orientul Mijlociu, India și China.
Două 11-lea contemporanii, Abu Bakr al-Karaji în Bagdad și Jia Xian (un tribunal Chinez eunuc) a studiat polinoame de grad ridicat, a găsit metode pentru extragerea rădăcini, și a descoperit ceea ce noi numim astăzi triunghiul lui Pascal. Al-Karaji a dat prima dovadă cunoscută a formulei pentru suma cuburilor—de asemenea, unul dintre primele exemple cunoscute de dovadă completă prin inducție.,
sume de cuburi
când însumați cuburi de numere întregi succesive, găsiți rapid un model:
13 = 1, 13 + 2 3 = 9, 13 + 23 + 33 = 36, 13 + 23 + 33 +43 = 100, 13 +··· +53 = 225.acestea sunt toate pătrate perfecte, și nu doar orice pătrate perfecte, dar
12, 32 = (1 + 2)2, 62 = (1 + 2 + 3)2, 102 = (1 + 2 + 3 + 4)2, 152 = (1 + ··· + 5)2.
formula pentru suma de cuburi este ușor de ghicit:
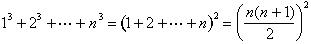
Aryabhata din Patna (în ceea ce este acum India) a descoperit această formulă în jur de 500 C. E., și se poate să fi fost cunoscut chiar mai devreme., Ar fi redescoperit de către Abu al-Saqr Abd al-Aziz ibn Uthman al-Qabisi în secolul al 10-lea Bagdad și din nou la începutul lunii 14-lea în Franța de către Levi ben Gerson. Nilakantha din Kerala (în sud-vestul Indiei) a dat o dovadă vizuală în 1500 care surprinde esența dovezii lui al-Karaji.
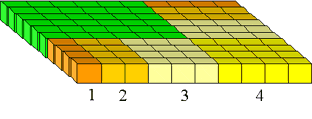
Figura 13: (1 + 2 + ··· + n) X(1 + 2+ ··· + n) pătrat.
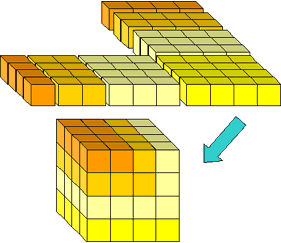
figura 14: rearanjarea blocurilor rămase într-un cub.
aceasta oferă etapa inductivă pentru dovada:
(1 + 2 + ··· + n) 2 = n3 + (1 + 2 +··· + (n-1)) 2.,în partea I a acestui articol, am văzut că ibn al-Haytham avea nevoie de sume de puteri a patra pentru a găsi volumul solidului obținut prin rotirea unei parabole în jurul unei linii perpendiculare pe axa de simetrie. A găsit o astfel de formulă. Deși nu avem nici o dovadă că și-a împins tehnica dincolo de Puterile a patra, abordarea sa poate fi folosită pentru a găsi formule pentru sume întregi consecutive pentru orice putere.al-Haytham a început cu formula pentru suma cuburilor. El a folosit-o pentru a bootstrap până la o formulă pentru sume de puteri a patra., regruparea astfel încât să putem obține sume de cuburi consecutive:
(13 + 23 + ··· + (k – 1)3 + k3 )(k + 1)
= (14 + 24 + ··· + (k – 1)4) + k4 ) + 13 + (13 + 23) + (13 + 23 + 33) + ···
+ (13 + 23 + ··· + (k – 1)3 ) + (13 + 23 + ··· + k3)
acum Vom folosi formula pentru suma de cuburi:
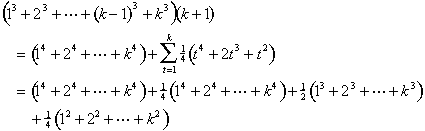
Vom consolida condiții similare și de a folosi formule pentru sume de cuburi și pătrate încă o dată:
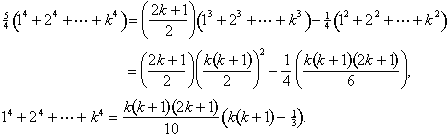
aceeași idee va lucra pentru a găsi o formulă pentru suma de-al cincilea competențe în ceea ce privește suma de-a patra puteri, și așa mai departe.,în secolul al XII-lea Bagdad și apoi independent în India și China din secolul al XIV-lea, matematicienii au descoperit și exploatat o proprietate remarcabilă a triunghiului lui Pascal. Începând de la margine, coborâți orice diagonală care se îndreaptă spre sud-vest, adăugând intrările. Oriunde te-ai opri, suma acestor numere este numărul următor la sud-est:
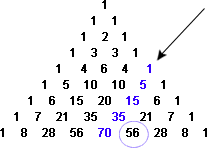
Figura 15: suma de termeni pe o sud-vest diagonală (1+5+15+35) este egal cu următorul termen de sud-est (56).putem exprima acest lucru în termeni de polinoame., Vom defini un polinom de gradul n:
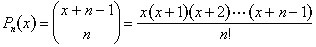
Această proprietate de diagonala sume implică faptul că pentru numere întregi pozitive n si k, avem mereu
Pn(1) + Pn(2) + ··· + Pn(k) = Pn + 1(k).
x4 = 24P4(x) – 36P3(x) + 14P2 (x) – P1(x).
rezultă că
14 + 24 + ··· + k4 = 24P5(k) – 36P4(k) + 14P3(k) – P2(k).
Această relație fundamentală pentru coeficienți binomiali apărut pentru prima dată în Al-Bahir fi ‘l Hisab (Stralucitoare Tratat de Calcul) scris de al-Samaw’ al în 1144 în prezent-zi Irak., De asemenea, pot fi găsite în Siyuan Yujian scris de Zhu Shijie în 1303, în China, și Ganita Kaumudi scris de Narayana Pandita în 1356 în India.remarcabil cum este această metodă, nu este cel mai bun mod de a găsi formule pentru sumele puterilor. Acest lucru a fost descoperit de matematicianul elvețian Jacob Bernoulli la începutul secolului al XVIII-lea. Timp de două mii de ani, matematicienii au folosit sume de formule de puteri pentru a calcula zonele. Bernoulli a folosit calculul integral pentru a găsi derivări simple ale formulelor suma puterilor. Dar asta e altă poveste.,
Resurse
Calinger, Ronald. O istorie contextuală a matematicii: la Euler. Upper Saddle River, N. J.: Prentice Hall, 1999.Dick, Thomas P. și Charles M. Patton. Calcul. Boston, Mass.: PWS Publishing, 1995.dijksterhuis, E. J. Arhimede. Tradus de C. Dikshoorn. 1938. Princeton, N. J.: Princeton University Press, 1987.
Heath, Thomas. O istorie a matematicii grecești. 2 vol. Oxford: Oxford University Press, 1921. Reimprimare: Dover, 1981.Katz, Victor J. O istorie a matematicii: o introducere. Ediția a 2-a. New York: Harper Collins, 1998.,
– – -. „Idei de calcul în Islam și India.”Mathematics Magazine 68-3 (1995): 163-174.Martzloff, Jean-Claude. O istorie a matematicii Chineze. Tradus de Stephen S. Wilson. New York: Springer-Verlag, 1998.Saraswathi, T. A. „dezvoltarea seriilor matematice în India după Bhaskara II.” Buletinul Institutului Național de științe 21 (1963): 320-343.Stein, Sherman. Arhimede: Ce A Făcut În Afară De Strigătul Eureka? Washington, D. C.: The Mathematical Association of America, 1999.