Assim, o PMF é uma medida da probabilidade, que nos dá a probabilidade de os valores possíveis para uma variável aleatória. Enquanto a notação acima é a notação padrão para o PMF de $X$, pode parecer confuso no início. O subscrito $X$ aqui indica que este é o PMF da variável aleatória $X$. Assim, por exemplo, $P_X (1)$ mostra a probabilidade de que $X=1$., Para entender melhor todos os conceitos acima, vamos olhar para alguns exemplos.

exemplo
Embora o PMF seja geralmente definido para valores no intervalo, às vezes é conveniente estender o PMF de $X$ para todos os números reais. Se $x \notin R_X$, podemos simplesmente escrever $P_X(x)=P (X=x)=0$. Assim, em geral, podemos escrever \begin{equation} \nonumber P_X(x) = \left\{ \begin{array}{l} P(X=x) & \quad \text{se $x$ é em } R_X\\ 0 & \quad \text{senão} \end{array} \right. \end{equation}

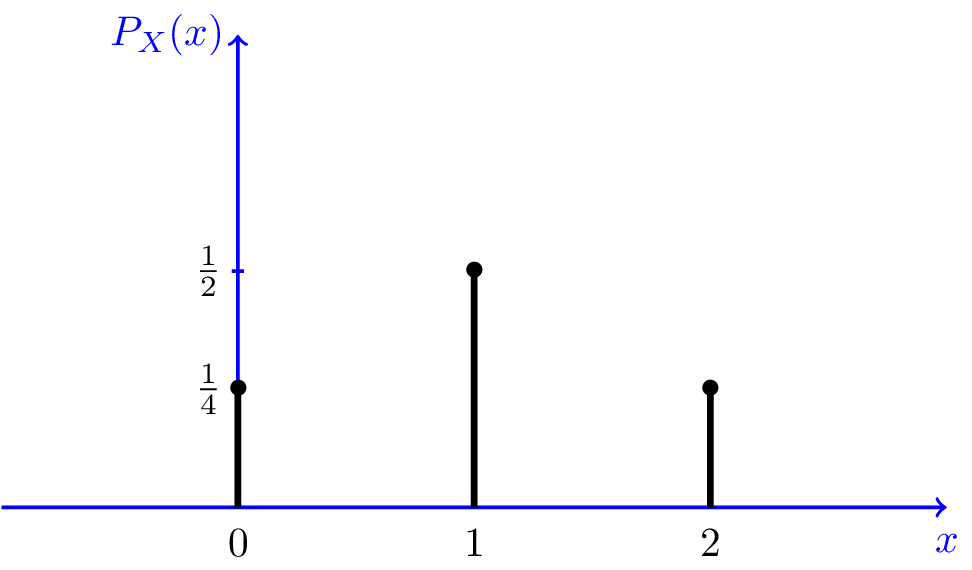
para visualizar melhor o PMF, podemos desenhá-lo. Figura 3.,1 mostra o PMF da variável aleatória acima $X$. Como vemos,a variável aleatória pode levar três valores possíveis $ 0,1 e $ 2$. A figura também indica claramente que o evento $X=1$ é duas vezes mais provável que os outros dois valores possíveis. A Figura pode ser interpretada da seguinte forma: Se nós repita o experimento aleatório (jogar uma moeda duas vezes) um grande número de vezes e, em seguida, cerca de metade das vezes que observar $X=1$, cerca de um quarto das vezes observamos $X=0$, e cerca de um quarto das vezes observamos $X=2$.

para variáveis aleatórias discretas, a PMF também é chamada de distribuição de probabilidade. Assim, quando perguntado para encontrar a distribuição de probabilidade de uma variável aleatória discreta $X$, podemos fazer isso encontrando seu PMF. A função de distribuição de frases é geralmente reservada exclusivamente para a função de distribuição cumulativa CDF (como definido mais tarde no livro). A distribuição de palavras, por outro lado, neste livro é usado em um sentido mais amplo e pode se referir a PMF, função de densidade de probabilidade (PDF), ou CDF.,

exemplo

I have an unfair coin for which $P(H)=P$, where $0

considere uma variável aleatória discreta $X$ with Range$(X)=R_X$. Note que, por definição, o PMF é uma medida de probabilidade, de modo que satisfaz todas as propriedades de uma medida de probabilidade. Em particular, temos

• $0\leq P_X(x) \leq 1$ para todo $x$ e
• $\sum_{x \in R_X} P_X(x)=1$.

note também que para qualquer conjunto $a \subconjunto R_X$, podemos encontrar a probabilidade de que $X \em$ usando o PMF$P(X \in a)=\sum_{x \in a} P_X(x).,$$

Exemplo

Para a variável aleatória $Y$, no Exemplo 3.4,

1. Verifique se $\sum_{y \in R_Y} P_Y(y)=1$.
2. If $p=\frac{1}{2}$, find $P( 2\leq Y