Parte I
O Desenvolvimento do Cálculo
a História tem uma forma de focar crédito para qualquer invenção ou descoberta em um ou dois indivíduos em um tempo e lugar. A verdade não é tão simples. Quando damos a impressão de que Newton e Leibniz criaram o cálculo a partir de tecido inteiro, prestamos um mau serviço aos nossos alunos. Newton e Leibniz eram brilhantes, mas nem eles eram capazes de inventar ou descobrir cálculo.,
O corpo da matemática que conhecemos como cálculo desenvolveu-se ao longo de muitos séculos em muitas partes diferentes do mundo, não apenas na Europa Ocidental, mas também na Grécia antiga, Oriente Médio, Índia, China e Japão. Newton e Leibniz se basearam em um vasto conjunto de conhecimentos sobre temas em Cálculo Diferencial e integral. O assunto continuaria a evoluir e a desenvolver-se muito depois das suas mortes. O que marca Newton e Leibniz é que eles foram os primeiros a declarar, entender e efetivamente usar o Teorema Fundamental do cálculo., Não há duas pessoas que moveram a nossa compreensão do cálculo tão longe ou tão rápido. Mas os problemas que estudamos em cálculo-áreas e volumes, taxas relacionadas, posição / velocidade / aceleração, séries infinitas, equações diferenciais—tinham sido resolvidos antes do nascimento de Newton ou Leibniz.
demorou cerca de 1.250 anos para passar da integral de um quadrático para a de um polinômio de quarto grau. Mas a consciência desta luta pode ser um lembrete útil para nós. Os grandes resultados que resolvem tantos problemas tão facilmente (a integração de um polinômio sendo um exemplo principal) escondem uma longa luta conceitual., Quando saltamos muito rápido para o algoritmo mágico e não reconhecemos o esforço que foi para a sua criação, arriscamo-nos a arrastar os nossos alunos para além dessa compreensão conceptual.
Este artigo explora a história do cálculo antes de Newton e Leibniz: as pessoas, problemas e lugares que fazem parte da rica história do cálculo.
Encontrar o Volume de um Parabaloid
Abu Ali al-Hasan ibn al-Haytham (também conhecido pela forma Latinizada de seu nome: Alhazen) foi um dos grandes matemáticos Árabes. Ele nasceu em Basra, Pérsia, agora no sudeste do Iraque., Algum tempo depois de 996, mudou-se para o Cairo, Egito, onde se associou à Universidade de Al-Azhar, fundada em 970. Ele escreveu mais de 90 livros, e é mais famoso por seu trabalho em astronomia e óptica. Seu interesse em matemática variou sobre álgebra, geometria e teoria dos números. Concentro-me nele porque ele é a primeira pessoa que conheço a ter integrado um polinômio de quarto grau.
claro, ele não o expressou dessa forma. Cerca de 250 a. C.,, Arquimedes escreveu sobre Conoides e esferoides, um livro que, entre outras coisas, demonstrou como encontrar o volume de um parabalóide, o sólido da revolução que você obtém quando você roda uma parábola em torno de seu eixo (ver Figura 1)., Em particular, se a e b são constantes positivas, e nós o tomamos a região delimitada acima, o gráfico da parábola abaixo do eixo x, e à direita de x = a (ver Figura 2), e girar esta região em torno do eixo x, temos o sólido de revolução, cujo volume é
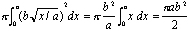
Em outras palavras, o volume é exatamente a metade do cilindro que você ganha se você girar o retângulo de comprimento a e altura b em torno do eixo x.
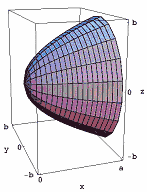
Figura 1: o parabalóide.

Figura 1: o parabalóide.,
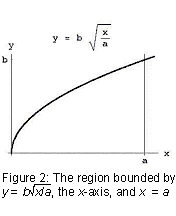

A parte difícil deste cálculo, algo que levou um matemático de Arquimedes estatura para perceber, é que o problema de encontrar o volume de um parabaloid pode ser reduzido para encontrar a área sob uma linha reta (a integral de x de 0 para um).,no mundo árabe do século X, Arquimedes sobre Conóides e esferóides era desconhecido, mas Thabit ibn Qurra do Sul da Turquia e Abu Sahl al-Kuhi do Norte do Irã descobriram suas próprias provas do volume de um parabalóide. Ibn al-Haytham leu seu trabalho e fez a si mesmo a pergunta: e se nós girarmos esta região em torno da linha x = a em vez do eixo x?
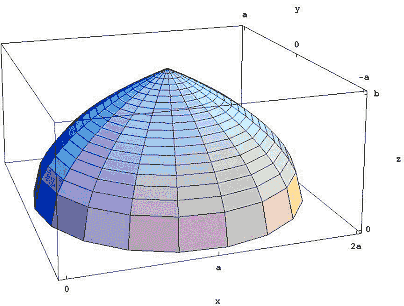
Figura 3: Rodar a região em torno da linha x = a.
O resultado é a Islâmica-olhando cúpula mostrado na Figura 3., Ibn al-Haytham mostrou que o seu volume é de 8/15ths do volume do cilindro que você começa quando você girar o retângulo de comprimento a e altura b em torno de x = a. Na notação moderna de cálculo, o cálculo deste volume torna-se
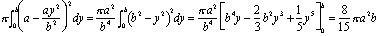
Mas ibn al-Haytham viveu há cerca de 700 anos antes de as fórmulas integrais viria a ser conhecido. Ele encontrou o volume empilhando discos. Se cortarmos a cúpula em discos nv, cada um com espessura b/n, então o disco I do fundo tem um raio a – ai2/n2 e volume (b/n) p (A – ai2/n2)2 (ver Figura 4)., O volume total desta pilha de discos é
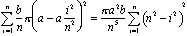
tudo o que resta é encontrar uma fórmula—em termos de n—para a soma. Então vemos o que acontece quando n se aproxima do infinito. Expandimos a soma e retiramos os poderes constantes de n:
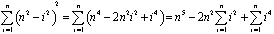
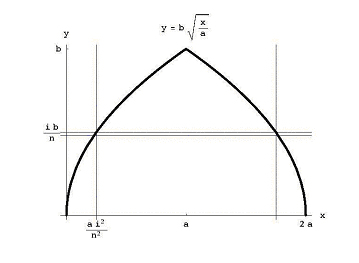
Figura 4: a fatia horizontal através da cúpula.
para ibn al-Haytham como para matemáticos no Oriente Médio, Sul Da Ásia e leste Da Ásia, o problema do cálculo de áreas e volumes veio para o problema de encontrar somas de poderes de inteiros consecutivos., Ibn al-Haytham foi um dos muitos matemáticos em muitos lugares diferentes que conseguiram resolver este problema. Ele mostrou que:
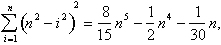
O volume da cúpula:
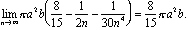
Como é que ele encontrar essa soma? Essa história abrange mais de dois mil anos e três continentes.
Part II
Archimedes and Sums of Squares
No description of calculus before Newton and Leibniz could be complete without an account of the contributions of Archimedes, the Greek Sicilian who was born around 287 B. C. and died in 212 B. C., durante o cerco Romano a Siracusa. Vamos olhar para um dos muitos problemas de cálculo que ele estudou.
é comum creditar Arquimedes com as primeiras agitações do cálculo integral. Entre as dificuldades enfrentadas e solucionadas estão encontrando áreas sob parábolas e dentro de espirais, e encontrar o volume da esfera, segmentos esféricos, e o parabaloid (o sólido de revolução obtido pela rotativo, uma parábola em torno de seu eixo). He also showed how to compute the slope of a line tangent to a spiral, the first glimmer of differential calculus.,
A beleza do cálculo como sabemos agora vem de sua simplicidade. O Teorema Fundamental do cálculo permite-nos resolver problemas muito difíceis aplicando procedimentos de cálculo simples que são justificados pelo Teorema Fundamental. Arquimedes não tinha estes, então ele teve que confiar em princípios básicos e, com muita ingenuidade, chegar a soluções inteligentes.Arquimedes encontrou volumes do parabalóide e outros sólidos usando um argumento de equilíbrio no qual ele comparou os momentos de diferentes sólidos., Ele calculou a área sob uma parábola e não pelo método usual de aproximá-lo por uma soma de quadrados, mas através de um geométrica de observação que permitiu reduzir o problema para encontrar a soma de uma série geométrica. Este é um dos vários usos importantes de séries geométricas que contribuíram para o desenvolvimento do cálculo.
O problema que eu quero focar é o de encontrar a área dentro de uma espiral. Em coordenadas polares, a espiral Arquimedeana (ver Figura 5) é r = kq para alguma constante K., Em coordenadas retangulares, é a curva com equações paramétricas: x(t) = k · t · cos t, y(t) = k · t · sin t, t >= 0.
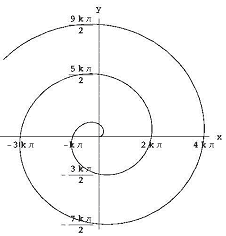
Figura 5: a espiral Arquimedeana
Arquimedes empregou o que passou a ser conhecido como o “método de exaustão.”A ideia é aproximar a área, utilizando sempre peças menores, cuja área pode ser encontrada exatamente, e então, para provar que um determinado valor é a resposta, mostrando que qualquer coisa menor é muito pequena e qualquer coisa maior é muito grande.,
Arquimedes atributos este método de Eudoxus de Cnidus (408-355 a.c.), que provou que o volume de qualquer pirâmide ou cone é um terço da área da base multiplicada pela altura. Enquanto Eudoxo encontrou a primeira prova, este resultado é ainda mais antigo: foi encontrado por Demócrito (C. 465-375 A. C.). A fórmula para o volume de uma pirâmide também foi descoberta na Índia antiga, e temos registro dela no Livro Chinês Chiu Chang Suan Ching (nove capítulos sobre a arte matemática) que pode ter sido escrito já em 150 a. C.,
mesmo antes que alguém pudesse provar esta fórmula, achando que era necessário pensar na pirâmide como feita de fatias finas, três conjuntos dos quais poderiam ser reconfigurados para fazer um bloco retangular. Mais tarde neste artigo veremos como essa geometria mental tridimensional levou Arquimedes à fórmula que ele precisava para encontrar a área da espiral.
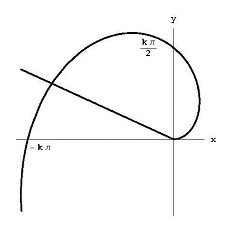
Figura 6: a área delimitada pela espiral Arquimedeana e pelo raio q = q1.,
a Aproximação da Área de uma Espiral
Para encontrar a área delimitada pela espiral e o raio q = q1, como mostrado na Figura 6, podemos dividir o ângulo entre os raios em n ângulos pequenos de tamanho p1 / n. Se nós olharmos a om pedaço de ângulo, a espiral é a distância da origem aumenta de k(i – 1) t1/ n ki q1/ n. Isto significa que a nossa área encontra-se dentro do setor de raio ki q 1/ n. A nossa área totalmente inclui o setor de círculo de raio k(i – 1) t1/ n.,
O ângulo q1/ n representa q1 / 2 p n de um círculo completo, de modo que a área do setor é em algum lugar entre
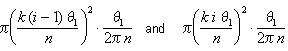
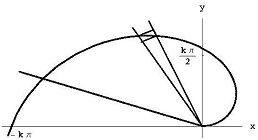
Figura 7: O setor entre q = k(i – 1)t1/n e q=ki q1/n
Quando nós simplificar esses limites, vemos que a área do i-ésimo segmento situa-se entre k2q 13 (i – 1)2/2n3 e k2q13 i2 /2n3. A área total situa – se entre
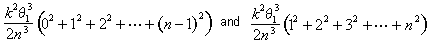
neste ponto, Arquimedes derivou uma fórmula sucinta para a soma dos primeiros quadrados n-1:
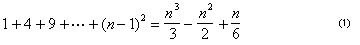 .,
.,
A área sob a espiral está em algum lugar entre
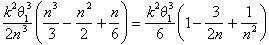
e
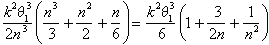
Como Arquimedes agora argumentou, o único número que se encontra entre estes limites para todos os valores de n é k2 p13 /6.
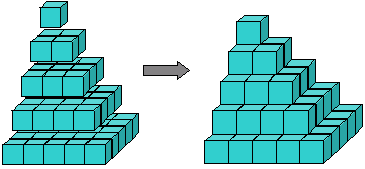
Figura 8: A pirâmide de praças
A Fórmula para a Soma dos Quadrados
A fórmula para a soma dos quadrados pode não ter sido novo Arquimedes, e há evidências de que poderia ter sido descoberto sobre o mesmo tempo na Índia. Sabemos que foi redescoberto muitas vezes., As provas mais antigas, incluindo a prova de Arquimedes, são todas geométricas.
podemos visualizar a soma dos quadrados como uma pirâmide construída a partir de cubos (Figura 8). Arquimedes mostrou como tomar três dessas pirâmides juntamente com uma camada triangular de blocos representando 1+2···+ (n – 1) e encaixá – los juntos para obter um bloco de cubos n x n x (n-1). Em outras palavras, ele mostrou que
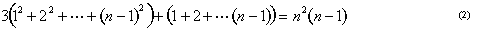 .
.
A Fórmula 1+2+···+ (n – 1)=n (n-1)/2 é muitas vezes atribuído a Gauss. A história é que ele descobriu quando seu professor ordenou que ele adicionasse os inteiros de 1 a 100., Na verdade, é uma fórmula antiga. Ela pode ser encontrada, por exemplo, na Índia em um manuscrito de Jain de 300 a. C.: ela teria sido parte da própria instrução matemática de Arquimedes. Tem uma prova geométrica muito simples, como mostrado na Figura 9.
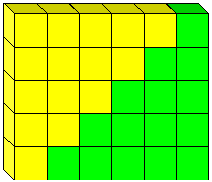
Figura 9: A prova de que 2 = n(n-1)
ainda temos que provar-se a equação (2), mas uma vez que sabemos que é verdadeiro, podemos combiná-lo com a fórmula para a soma dos primeiros n – 1 números inteiros para obter
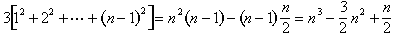
Dividir ambos os lados por 3, e obtemos a equação (1).,
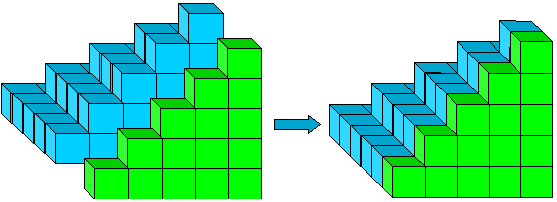
Figura 10: 12+22+···+(n – 1)2 +1+2+···+(n – 1).
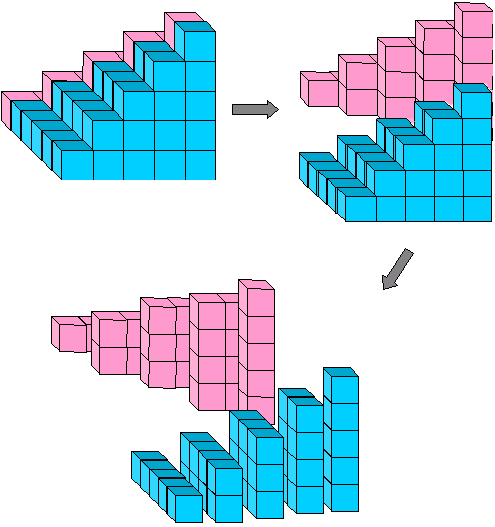
Figura 11: 1· 2 + 2·3 + 3·4 +···+ (n-1)n = 2
A equação algébrica que corresponde a essa imagem é
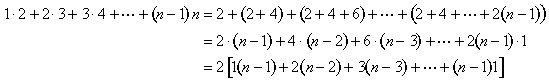
Estas peças se encaixam em torno da pirâmide verde na Figura 8, para que mais uma pirâmide invertida, conclui a n x n x (n – 1) bloco (Figura 12):
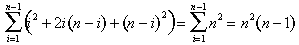
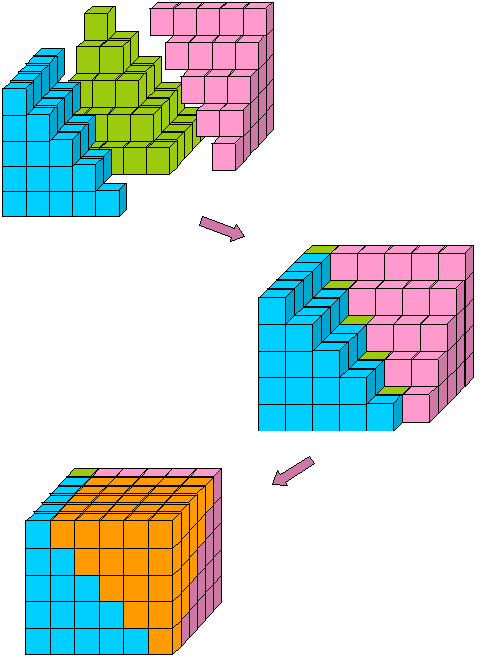
Figura 12: A n x n x (n – 1) bloco montado a partir de três somas de quadrados e uma soma de números inteiros.,
somas de cubos
você pode pensar que tendo visto o quão útil é a soma da fórmula dos quadrados, Arquimedes teria então encontrado a fórmula para a soma dos cubos. Levou mais de mil anos antes de alguém o fazer. O problema é que as somas dos quadrados são fáceis de ver geometricamente. Somas de cubos podem ser visualizadas, mas o objeto que você quer colocá-los juntos para formar é quadidimensional. Mas como veremos na Parte III, quando a Europa estava na Idade Média, matemáticos no Oriente Médio, Índia e China já o tinham feito.,nas duas primeiras partes deste artigo, vimos como Arquimedes e ibn al-Haytham usavam fórmulas para somas de poderes para avaliar áreas e volumes. A partir do século XI, matemáticos árabes, chineses e indianos começaram a descobrir técnicas que lhes permitiriam encontrar a área sob qualquer polinômio. Mas antes que alguém pudesse descobrir tais fórmulas, eles tinham que inventar polinômios. Polinômios quadráticos e cúbicos existiram por muito mais de mil anos, mas expressos como áreas e volumes., Nem sequer ficou claro o que significaria uma quarta potência. Polinômios de alto grau emergiram quase simultaneamente por volta do ano 1000 no Oriente Médio, Índia e China.dois contemporâneos do século XI, Abu Bakr al-Karaji em Bagdá e Jia Xian (um eunuco da corte chinesa) estudaram polinômios de alto grau, encontraram métodos para extrair raízes, e descobriram o que hoje chamamos de triângulo de Pascal. Al-Karaji deu a primeira prova conhecida da fórmula para a soma dos cubos—também um dos primeiros exemplos conhecidos de uma prova completa por indução.,
Soma de Cubos
Quando você soma de cubos de sucessivos números inteiros, a encontrar rapidamente um padrão:
13 = 1, 13 + 2 3 = 9, 13 + 23 + 33 = 36, 13 + 23 + 33 +43 = 100, 13 +··· +53 = 225.
Estes são todos os quadrados perfeitos, e não de qualquer quadrados perfeitos, mas
12, 32 = (1 + 2)2, 62 = (1 + 2 + 3)2, 102 = (1 + 2 + 3 + 4)2, 152 = (1 + ··· + 5)2.
A fórmula para a soma dos cubos é fácil de adivinhar:
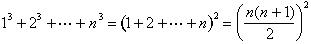
Aryabhata of Patna (in what is now India) descobriu esta fórmula em torno de 500 C. E., e pode ter sido conhecido ainda antes., Seria redescoberto por Abu al-Saqr Abd al-Aziz ibn Uthman al-Qabisi em Bagdá do século X e novamente no início do século XIV na França por Levi ben Gerson. Nilakantha de Kerala (no sudoeste da Índia) deu uma prova visual em 1500 que captura a essência da prova de al-Karaji.
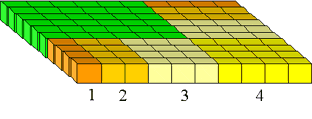
Figura 13: O (1 + 2 + ··· + n)X(1 + 2+ ··· + n) praça.
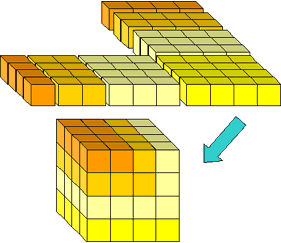
Figura 14: rearranjar os blocos restantes num cubo.
isto fornece o passo indutivo para a prova:
(1 + 2 + ··· + n) 2 = n3 + (1 + 2 +··· + (n-1)) 2.,na Parte I deste artigo, vimos que ibn al-Haytham precisava de somas de quatro potências para encontrar o volume do sólido obtido girando uma parábola em torno de uma linha perpendicular ao eixo de simetria. Ele encontrou uma fórmula assim. Embora não tenhamos provas de que ele empurrou a sua técnica para além das quatro potências, a sua abordagem pode ser usada para encontrar fórmulas para somas de inteiros consecutivos para qualquer poder.
Al-Haytham começou com a fórmula para a soma dos cubos. Ele usou-o para criar uma fórmula para somas de quatro poderes., reagrupamento de modo a obtermos soma de cubos consecutivos:
(13 + 23 + ··· + (k – 1)3 + k3 )(k + 1)
= (14 + 24 + ··· + (k – 1)4) + k4 ) + 13 + (13 + 23) + (13 + 23 + 33) + ···
+ (13 + 23 + ··· + (k – 1)3 ) + (13 + 23 + ··· + k3)
agora usamos a fórmula para a soma dos cubos:
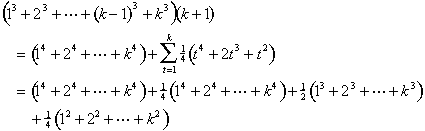
Nós consolidar termos semelhantes e utilizar as fórmulas para a soma dos cubos e quadrados, mais uma vez:
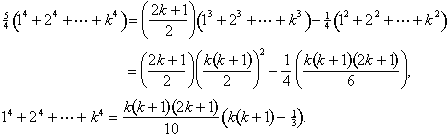
A mesma ideia que vai trabalhar para encontrar uma fórmula para a soma do quinto poderes em termos da soma de quarta poderes, e assim por diante.,os matemáticos descobriram e exploraram uma notável propriedade do triângulo de Pascal. A partir da borda, desça qualquer diagonal que vá para sudoeste, adicionando as entradas. Onde quer que pare, a soma destes números é o próximo número a sudeste:
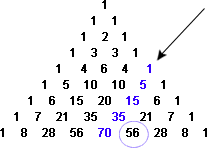
Figura 15: a soma dos Termos numa diagonal sudoeste (1+5+15+35) é igual ao próximo termo para o Sudeste (56).
podemos expressar isso em termos de polinômios., Definimos um polinômio de grau n:
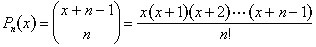
Esta propriedade da diagonal somas implica que para números inteiros positivos n e k, temos sempre
Pn(1) + Pn(2) + ··· + Pn(k) = Pn + 1(k).
x4 = 24P4(x) – 36P3(x) + 14P2 (x) – P1(x).
segue-se que
14 + 24 + ··· + k4 = 24P5(k) – 36P4(k) + 14P3(k) – P2(k).esta relação fundamental para os coeficientes binomiais apareceu pela primeira vez em Al-Bahir fi’l Hisab (Tratado brilhante sobre cálculo) escrito por al-Samaw’Al em 1144 no atual Iraque., Ele também pode ser encontrado em Siyuan Yujian escrito por Zhu Shijie em 1303, na China, e o Ganita Kaumudi escrito por Narayana Pandita em 1356, na Índia.por mais notável que este método seja, não é a melhor maneira de encontrar fórmulas para as somas de poderes. Isto foi descoberto pelo matemático suíço Jacob Bernoulli no início do século XVIII. Durante dois mil anos, matemáticos usaram somas de fórmulas de poderes para calcular áreas. Bernoulli usou o cálculo integral para encontrar derivações simples da soma das fórmulas de poderes. Mas isso é outra história.,
recursos
Calinger, Ronald. A Contextual History of Mathematics: To Euler. Upper Saddle River, N. J.: Prentice Hall, 1999.Dick, Thomas P., and Charles M. Patton. Calculo. Boston, Mass.: PWS Publishing, 1995.Dijksterhuis, E. J. Archimedes. Translated by C. Dikshoorn. 1938. Princeton, N. J.: Princeton University Press, 1987.Heath, Thomas. A History of Greek Mathematics. 2 vols. Oxford: Oxford University Press, 1921. Reprint: Dover, 1981.
Katz, Victor J. A History of Mathematics: An Introduction. 2nd edition. New York: Harper Collins, 1998.,
– – -. “Ideas of Calculus in Islam and India.”Mathematics Magazine 68-3 (1995): 163-174.Martzloff, Jean-Claude. A History of Chinese Mathematics. Translated by Stephen S. Wilson. New York: Springer-Verlag, 1998.
Saraswathi, T. A. “The Development of Mathematical Series in India After Bhaskara II.” Bulletin of the National Institute of Sciences 21 (1963): 320-343.Stein, Sherman. O Que Fez Ele Além De Cry Eureka? Washington, D. C.: The Mathematical Association of America, 1999.