Part I
Lo sviluppo del calcolo
La storia ha un modo di focalizzare il credito per qualsiasi invenzione o scoperta su uno o due individui in un tempo e luogo. La verità non è così pulito. Quando diamo l’impressione che Newton e Leibniz abbiano creato il calcolo da tutto il tessuto, facciamo un cattivo servizio ai nostri studenti. Newton e Leibniz erano brillanti, ma nemmeno loro erano in grado di inventare o scoprire il calcolo.,
Il corpo della matematica che conosciamo come calcolo si è sviluppato nel corso di molti secoli in molte parti diverse del mondo, non solo l’Europa occidentale, ma anche l’antica Grecia, il Medio Oriente, l’India, la Cina e il Giappone. Newton e Leibniz ha attirato su un vasto corpo di conoscenze su argomenti sia in calcolo differenziale e integrale. Il soggetto avrebbe continuato ad evolversi e svilupparsi molto tempo dopo la loro morte. Ciò che segna Newton e Leibniz è che furono i primi a dichiarare, comprendere e utilizzare efficacemente il Teorema fondamentale del Calcolo., Non ci sono due persone che hanno spostato la nostra comprensione del calcolo più lontano o più velocemente. Ma i problemi che studiamo nel calcolo-aree e volumi, velocità correlate, posizione/velocità/accelerazione, serie infinita, equazioni differenziali—erano stati risolti prima della nascita di Newton o Leibniz.
Ci sono voluti circa 1.250 anni per passare dall’integrale di un quadratico a quello di un polinomio di quarto grado. Ma la consapevolezza di questa lotta può essere un utile promemoria per noi. I grandi risultati di spazzamento che risolvono così tanti problemi così facilmente (l’integrazione di un polinomio è un primo esempio) nascondono una lunga lotta concettuale., Quando saltiamo troppo velocemente all’algoritmo magico e non riconosciamo lo sforzo che è andato nella sua creazione, rischiamo di trascinare i nostri studenti oltre quella comprensione concettuale.
Questo articolo esplora la storia del calcolo prima di Newton e Leibniz: le persone, i problemi e i luoghi che fanno parte della ricca storia del calcolo.
Trovare il volume di un parabaloide
Abu Ali al-Hasan ibn al-Haytham (noto anche con la forma latinizzata del suo nome: Alhazen) è stato uno dei grandi matematici arabi. Era nato a Bassora, in Persia, ora nel sud-est dell’Iraq., Qualche tempo dopo il 996, si trasferì al Cairo, in Egitto, dove divenne associato con l’Università di Al-Azhar, fondata nel 970. Ha scritto oltre 90 libri, ed è più famoso per il suo lavoro in astronomia e ottica. Il suo interesse per la matematica variava oltre algebra, geometria, e la teoria dei numeri. Mi concentro su di lui perché è la prima persona che conosco ad aver integrato un polinomio di quarto grado.
Certo, non l’ha espresso in questo modo. Intorno al 250 a. C.,, Archimede ha scritto Su Conoidi e Sferoidi, un libro che, tra le altre cose, ha dimostrato come trovare il volume di un parabaloide, il solido di rivoluzione che si ottiene quando si ruota una parabola attorno al suo asse (vedi Figura 1)., In particolare, se a e b sono costanti positive e prendiamo la regione delimitata in alto dal grafico della parabola sotto l’asse x, e a destra di x = a (vedi Figura 2) e ruotare questa regione attorno all’asse x, si ottiene il solido di rivoluzione di cui il volume è
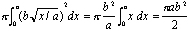
In altre parole, il volume è esattamente la metà di quella del cilindro che si ottiene se si fa ruotare il rettangolo di lunghezza e altezza b attorno all’asse x.
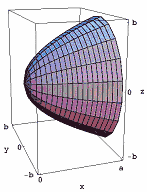
Figura 1: Il parabaloide.

Figura 1: Il parabaloide.,
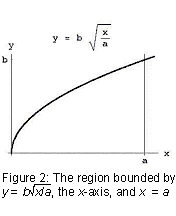

La parte più difficile di questo calcolo, qualcosa che ha preso un matematico di Archimede’ statura di realizzare, è che il problema di trovare il volume di un parabaloid può essere ridotta a quella di trovare l’area sotto una linea retta (l’integrale di x da 0 a).,
Nel mondo arabo del X secolo, Archimede’ Su Conoidi e Sferoidi era sconosciuto, ma Thabit ibn Qurra della Turchia meridionale e Abu Sahl al-Kuhi dell’Iran settentrionale avevano scoperto le proprie prove del volume di un parabaloide. Ibn al-Haytham ha letto il loro lavoro e si è posto la domanda: Cosa succede se ruotiamo questa regione attorno alla linea x = a invece dell’asse x?
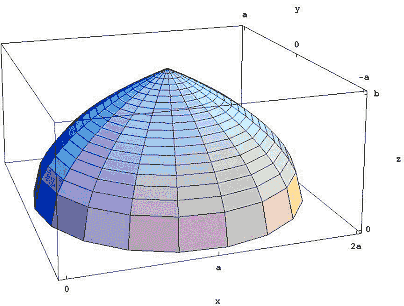
Figura 3: Ruotando la regione attorno alla linea x = a.
Il risultato è la cupola dall’aspetto islamico mostrata in Figura 3., Ibn al-Haytham ha mostrato che il suo volume è di 8/15ths del volume del cilindro che si ottiene quando si ruota il rettangolo di lunghezza e altezza b intorno a x = a. Nella notazione moderna di calcolo, il calcolo di questo volume diventa
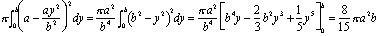
Ma ibn al-Haytham vissuto quasi 700 anni prima formule integrali di essere conosciuto. Ha trovato il volume impilando i dischi. Se tagliamo la cupola in dischi nv, ciascuno di spessore b / n, allora il disco ith dal basso ha raggio a – ai2/n2 e volume (b/n) p (a – ai2/n2)2 (vedi Figura 4)., Il volume totale di questa pila di dischi è
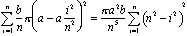
Tutto ciò che rimane è trovare una formula—in termini di n—per la somma. Vediamo quindi cosa succede quando n si avvicina all’infinito. Espandiamo il summand ed estraiamo le potenze costanti di n:
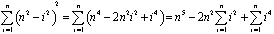
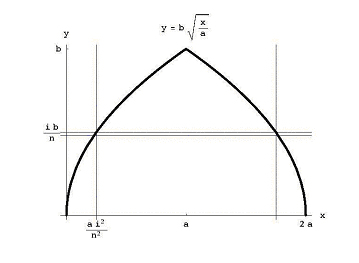
Figura 4: La fetta orizzontale attraverso la cupola.
Per ibn al-Haytham come per i matematici del Medio Oriente, dell’Asia meridionale e dell’Asia orientale, il problema del calcolo delle aree e dei volumi si ridusse al problema di trovare somme di potenze di interi consecutivi., Ibn al-Haytham è stato uno dei tanti matematici in molti luoghi diversi che è riuscito a risolvere questo problema. Ha mostrato che:
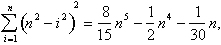
Il volume della cupola è:
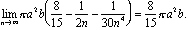
Come ha trovato questa somma? Quella storia si estende su duemila anni e tre continenti.
Parte II
Archimede e somme di quadrati
Nessuna descrizione del calcolo prima di Newton e Leibniz poteva essere completa senza un resoconto dei contributi di Archimede, il greco siciliano che nacque intorno al 287 a. C. e morì nel 212 a. C., durante l’assedio romano di Siracusa. Vedremo uno dei tanti problemi di calcolo che ha studiato.
È comune accreditare Archimede con i primi agitamenti del calcolo integrale. Tra i problemi che ha affrontato e risolto ci sono la ricerca di aree sotto le parabole e all’interno delle spirali, e la ricerca del volume della sfera, dei segmenti sferici e del parabaloide (il solido di rivoluzione ottenuto ruotando una parabola attorno al suo asse). Ha anche mostrato come calcolare la pendenza di una linea tangente a una spirale, il primo barlume di calcolo differenziale.,
La bellezza del calcolo come lo conosciamo ora deriva dalla sua semplicità. Il Teorema Fondamentale del Calcolo ci consente di risolvere problemi molto difficili applicando semplici procedure di calcolo giustificate dal Teorema Fondamentale. Archimede non aveva questi, quindi ha dovuto fare affidamento sui principi di base e, con una grande quantità di ingegno, trovare soluzioni intelligenti.
Archimede trovato volumi del parabaloide e altri solidi utilizzando un argomento di bilanciamento in cui ha confrontato i momenti di diversi solidi., Ha calcolato l’area sotto una parabola non con il solito metodo di approssimazione di una somma di quadrati, ma utilizzando un’osservazione geometrica che gli ha permesso di ridurre il problema di trovare la somma di una serie geometrica. Questo è uno dei numerosi usi importanti delle serie geometriche che hanno contribuito allo sviluppo del calcolo.
Il problema su cui voglio concentrarmi è quello di trovare l’area all’interno di una spirale. In coordinate polari, la spirale archimedea (vedi Figura 5) è r = kq per qualche costante k., In coordinate rettangolari, è la curva con equazioni parametriche: x(t) = k · t · cos t, y(t) = k · t · sin t, t >= 0.
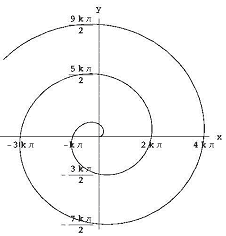
Figura 5: La spirale archimedea
Archimede impiegava quello che è diventato noto come il “metodo di esaurimento.”L’idea è di approssimare l’area usando pezzi sempre più piccoli la cui area può essere trovata esattamente, e quindi dimostrare che un particolare valore è la risposta mostrando che qualcosa di più piccolo è troppo piccolo e qualcosa di più grande è troppo grande.,
Archimede attribuisce questo metodo a Eudosso di Cnido (408-355 a. C.) che ha dimostrato che il volume di qualsiasi piramide o cono è un terzo dell’area della base moltiplicata per l’altezza. Mentre Eudosso ha trovato la prima prova, questo risultato è ancora più antico: è stato trovato da Democrito (c. 465-375 AC). La formula per il volume di una piramide fu scoperta anche nell’antica India, e ne abbiamo traccia nel libro cinese Chiu Chang Suan Ching (Nove capitoli sull’arte matematica) che potrebbe essere stato scritto già nel 150 a. C.,
Ancora prima che qualcuno potesse provare questa formula, trovandola richiedeva di pensare alla piramide come composta da fette sottili, tre serie delle quali potevano essere riconfigurate per creare un blocco rettangolare. Più avanti in questo articolo vedremo come questa geometria tridimensionale mentale ha portato Archimede alla formula di cui aveva bisogno per trovare l’area della spirale.
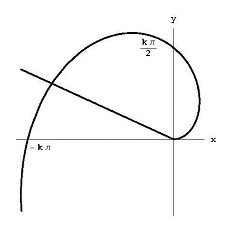
Figura 6: L’area delimitata dalla spirale archimedea e dal raggio q = q1.,
Approssimare l’Area della Spirale
Per trovare l’area delimitata dalla spirale e ray q = q1, come mostrato in Figura 6, si divide l’angolo tra i raggi n piccoli angoli di dimensioni t1 / n. Se guardiamo i-esimo pezzo di angolo, la spirale della distanza dall’origine aumenta da k(i – 1) t1/ n a ki t1/ n. Questo significa che il nostro territorio si trova all’interno del settore di raggio ki q 1/ n. La nostra area interamente comprende il settore di cerchio di raggio k(i – 1) t1/ n.,
L’angolo t1/ n rappresenta il t1 / 2 p n di un cerchio, in modo che l’area di questo settore è da qualche parte tra
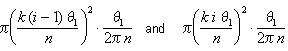
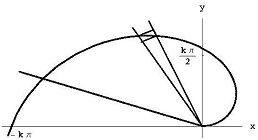
Figura 7: Il settore tra q = k(i – 1)t1/n e q=ki t1/n
Quando abbiamo semplificare questi limiti, vediamo che l’area dell’i-esimo segmento si trova tra k2q 13 (i – 1)2/2n3 e k2q13 i2 /2n3. L’area totale si trova tra
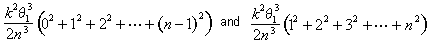
A questo punto, Archimede ha derivato una formula succinta per la somma dei primi quadrati n – 1:
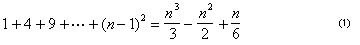 .,
.,
l’area sotto La spirale si trova da qualche parte tra
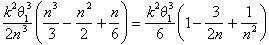
e
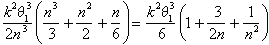
Come Archimede ora sostenuto, l’unico numero che si trova tra questi limiti per tutti i valori di n è k2 q13 /6.
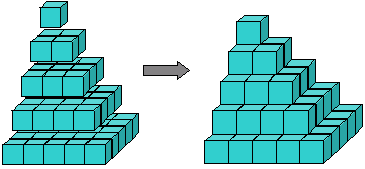
Figura 8: La piramide dei quadrati
La formula per la somma dei quadrati
La formula per la somma dei quadrati potrebbe non essere stata nuova per Archimede, e ci sono prove che potrebbe essere stata scoperta circa nello stesso periodo in India. Sappiamo che è stato riscoperto molte volte., Le prime prove, compresa la prova di Archimede, sono tutte geometriche.
Possiamo visualizzare la somma dei quadrati come una piramide costruita da cubi (Figura 8). Archimede ha mostrato come prendere tre di queste piramidi insieme a uno strato triangolare di blocchi che rappresentano 1+2···+ (n – 1) e inserirli insieme per ottenere un blocco di cubi n x n x (n – 1). In altre parole, ha mostrato che
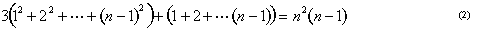 .
.
La formula 1+2+···+(n-1) = n (n – 1)/2 è spesso attribuito a Gauss. La storia è che l’ha scoperto quando il suo insegnante gli ha ordinato di aggiungere gli interi da 1 a 100., In realtà, è una formula antica. Può essere trovato, per esempio, in India in un manoscritto Jain da 300 B. C.: sarebbe stato parte di Archimede ‘ s propria istruzione matematica. Ha una prova geometrica molto semplice come mostrato in Figura 9.
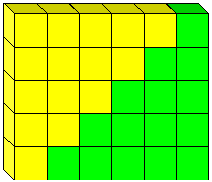
Figura 9: La prova che 2 = n(n-1)
Dobbiamo ancora dimostrare che l’equazione (2), ma una volta che sappiamo che è vero, si può combinare con la formula per la somma dei primi n – 1 numeri interi per ottenere
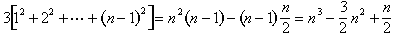
Dividere entrambi i lati da 3, e otteniamo l’equazione (1).,
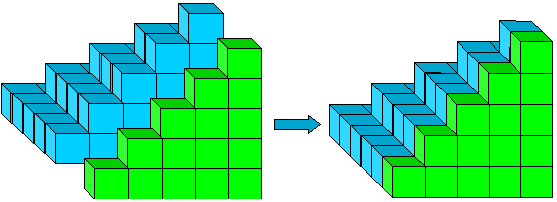
Figura 10: 12+22+···+(n – 1)2 +1+2+···+(n-1).
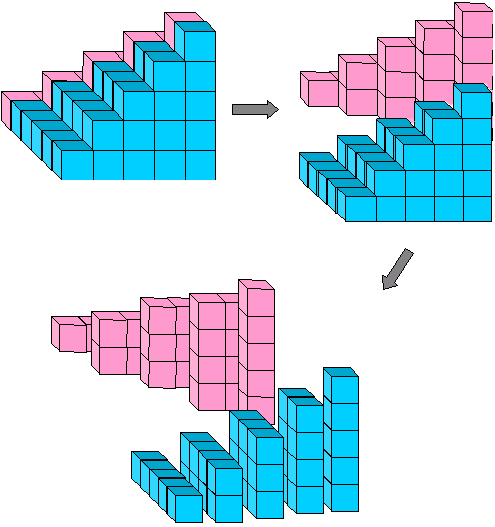
Figura 11: 1· 2 + 2·3 + 3·4 +···+ (n-1)n = 2
L’equazione algebrica che corrisponde a questa immagine
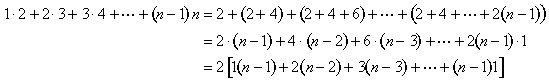
Questi pezzi si adattano intorno il verde piramide in Figura 8, in modo che ancora una piramide rovesciata, completa il n x n x (n – 1) blocco (Figura 12):
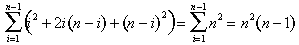
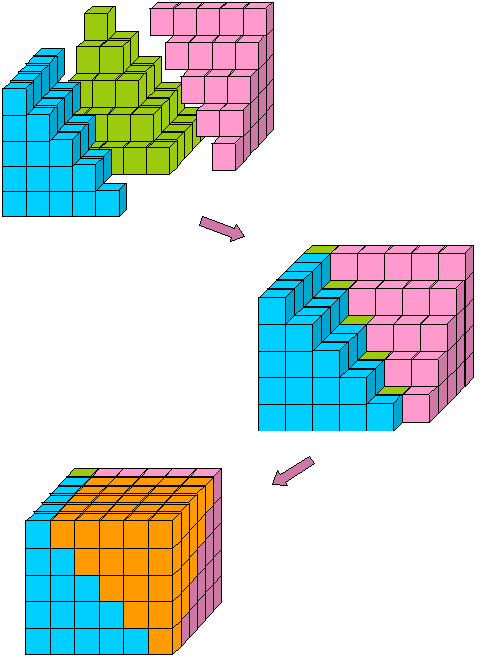
Figura 12: Il n x n x (n – 1) blocco assemblato da tre somme dei quadrati e una somma di numeri interi.,
Somme di cubi
Potresti pensare che avendo visto quanto sia utile la formula della somma dei quadrati, Archimede avrebbe quindi trovato la formula per la somma dei cubi. Ci sono voluti piu ‘ di mille anni prima che qualcuno lo facesse. Il problema è che le somme di quadrati sono facili da vedere geometricamente. Somme di cubi possono essere visualizzati, ma l’oggetto che si desidera metterli insieme per formare è quadridimensionale. Ma come vedremo nella Parte III, quando l’Europa era nel suo Medioevo i matematici del Medio Oriente, dell’India e della Cina lo avevano fatto tutti.,
Parte III
Somme di poteri
Nelle prime due parti di questo articolo, abbiamo visto come Archimede e ibn al-Haytham usavano formule per somme di poteri per valutare aree e volumi. A partire dal 11 ° secolo, arabi, cinesi, e matematici indiani ha cominciato a scoprire tecniche che consentirebbero loro di trovare l’area sotto qualsiasi polinomio. Ma prima che qualcuno potesse scoprire tali formule, dovevano inventare polinomi. Polinomi quadratici e cubici esistevano da oltre mille anni, ma espressi come aree e volumi., Non era nemmeno chiaro cosa significasse un quarto potere. Polinomi di grado superiore emersero quasi simultaneamente intorno all’anno 1000 in Medio Oriente, India e Cina.
Due contemporanei dell’XI secolo, Abu Bakr al-Karaji a Baghdad e Jia Xian (un eunuco di corte cinese) studiarono polinomi di alto grado, trovarono metodi per estrarre radici e scoprirono quello che oggi chiamiamo triangolo di Pascal. Al-Karaji ha dato la prima prova conosciuta della formula per la somma dei cubi-anche uno dei primi esempi noti di una prova completa per induzione.,
Somme di cubi
Quando si sommano cubi di interi successivi, si trova rapidamente un modello:
13 = 1, 13 + 2 3 = 9, 13 + 23 + 33 = 36, 13 + 23 + 33 +43 = 100, 13 +··· +53 = 225.
Questi sono tutti quadrati perfetti, e non solo quadrati perfetti, ma
12, 32 = (1 + 2)2, 62 = (1 + 2 + 3)2, 102 = (1 + 2 + 3 + 4)2, 152 = (1 + ··· + 5)2.
La formula per la somma dei cubi è facile da indovinare:
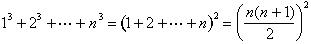
Aryabhata di Patna (in quella che oggi è l’India) scoprì questa formula intorno al 500 E. V., e potrebbe essere stata conosciuta anche prima., Sarebbe stato riscoperto da Abu al-Saqr Abd al-Aziz ibn Uthman al-Qabisi nel 10 ° secolo Baghdad e di nuovo all’inizio del 14 ° secolo in Francia da Levi ben Gerson. Nilakantha del Kerala (nel sud-ovest dell’India) ha dato una prova visiva nel 1500 che cattura l’essenza della prova di al-Karaji.
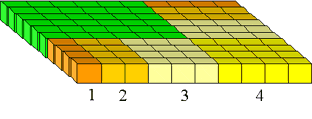
Figura 13: Il (1 + 2 + ··· + n) X(1 + 2+ ··· + n) quadrato.
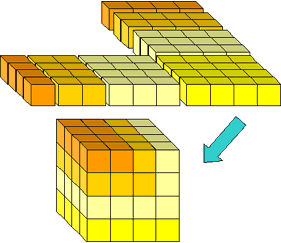
Figura 14: Riorganizzare i blocchi rimanenti in un cubo.
Questo fornisce il passo induttivo per la prova:
(1 + 2 + ··· + n) 2 = n3 + (1 + 2 +··· + (n-1)) 2.,
Somme di quarta potenza
Nella parte I di questo articolo, abbiamo visto che ibn al-Haytham aveva bisogno di somme di quarta potenza per trovare il volume del solido ottenuto ruotando una parabola attorno a una linea perpendicolare all’asse di simmetria. Ha trovato una tale formula. Mentre non abbiamo prove che abbia spinto la sua tecnica oltre i quarti poteri, il suo approccio può essere usato per trovare formule per somme di interi consecutivi a qualsiasi potere.
Al-Haytham ha iniziato con la formula per la somma dei cubi. Lo ha usato per bootstrap fino a una formula per somme di quarta potenza., il raggruppamento in modo che possiamo ottenere somme di cubi consecutivi:
(13 + 23 + ··· + (k – 1)3 + k3 )(k + 1)
= (14 + 24 + ··· + (k – 1)4) + k4 ) + 13 + (13 + 23) + (13 + 23 + 33) + ···
+ (13 + 23 + ··· + (k – 1)3 ) + (13 + 23 + ··· + k3)
ora usiamo la formula per la somma di cubi:
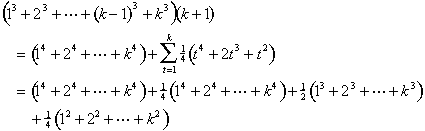
Ci consolidare i termini simili e utilizzare le formule per la somma dei cubi e quadrati, una volta di più:
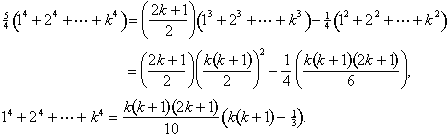
La stessa idea si metterà a lavoro per trovare una formula per la somma di quinto poteri in termini di somma di quarto poteri, e così via.,
Potenze superiori
Nel 12 ° secolo Baghdad e poi in modo indipendente nel 14 ° secolo India e Cina, matematici scoperto e sfruttato una notevole proprietà del triangolo di Pascal. Partendo dal bordo, scendere qualsiasi diagonale che si dirige a sud-ovest, aggiungendo le voci. Ovunque ci si fermi, la somma di questi numeri è il numero successivo a sud-est:
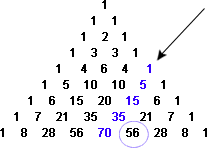
Figura 15: La somma dei termini su una diagonale sud-ovest (1+5+15+35) è uguale al termine successivo a sud-est (56).
Possiamo esprimerlo in termini di polinomi., Definiamo un polinomio di grado n:
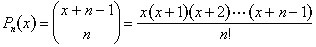
Questa proprietà delle somme diagonali implica che per interi positivi n e k, abbiamo sempre
Pn(1) + Pn(2) + ··· + Pn(k) = Pn + 1(k).
x4 = 24P4 ( x) – 36P3(x) + 14P2 (x) – P1(x).
Ne consegue che
14 + 24 + ··· + k4 = 24P5 ( k) – 36P4(k) + 14P3(k) – P2(k).
Questa relazione fondamentale per i coefficienti binomiali apparve per la prima volta in Al-Bahir fi’l Hisab (Shining Treatise on Calculation) scritto da al-Samaw’al nel 1144 nell’attuale Iraq., Può anche essere trovato in Siyuan Yujian scritto da Zhu Shijie nel 1303 in Cina, e il Ganita Kaumudi scritto da Narayana Pandita nel 1356 in India.
Notevole come questo metodo è, non è il modo migliore di trovare formule per le somme di poteri. Che è stato scoperto dal matematico svizzero Jacob Bernoulli all’inizio del 18 ° secolo. Per duemila anni, i matematici avevano utilizzato somme di formule di poteri per calcolare le aree. Bernoulli ha usato il calcolo integrale per trovare semplici derivazioni della somma delle formule di potenze. Ma questa è un’altra storia.,
Risorse
Calinger, Ronald. Una storia contestuale della matematica: a Eulero. Upper Saddle River, N. J.: Prentice Hall, 1999.
Dick, Thomas P., e Charles M. Patton. Calcolo. Boston, Messa.: PWS Publishing, 1995.
Dijksterhuis, E. J. Archimede. Tradotto da C. Dikshoorn. 1938. Princeton, N. J.: Princeton University Press, 1987.
Heath, Thomas. Una storia della matematica greca. 2 voll. Oxford: Oxford University Press, 1921. Ristampa: Dover, 1981.
Katz, Victor J. Una storia della matematica: Un’introduzione. 2a edizione. New York: Harper Collins, 1998.,
– – -. “Idee di calcolo nell’Islam e in India.”Mathematics Magazine 68-3 (1995): 163-174.
Martzloff, Jean-Claude. Una storia della matematica cinese. Tradotto da Stephen S. Wilson. New York: Springer-Verlag, 1998.
Saraswathi, TA “Lo sviluppo delle serie matematiche in India dopo Bhaskara II.” Bollettino dell’Istituto Nazionale delle Scienze 21 (1963): 320-343.
Stein, Sherman. Archimede: Cosa ha fatto oltre a piangere Eureka? Washington, DC: The Mathematical Association of America, 1999.