Donc, le CMR est une mesure de probabilité qui nous donne les probabilités des valeurs possibles pour une variable aléatoire. Bien que la notation ci-dessus soit la notation standard pour le PMF de X X$, cela peut sembler déroutant au premier abord. L’indice $X indicates indique ici que C’est le PMF de la variable aléatoire X X.. Ainsi, par exemple, $P_X( 1) shows montre la probabilité que $X=1.., Pour mieux comprendre tous les concepts ci-dessus, regardons quelques exemples.

exemple
bien que le PMF soit généralement défini pour des valeurs dans la plage, il est parfois pratique d’étendre le PMF de X X $à tous les nombres réels. Si $x \notin R_X$, nous pouvons simplement écrire $P_X(x)=P (X=x)=0.. Ainsi, dans l’ensemble, on peut écrire \begin{equation} \nonumber P_X(x) = \left\{ \begin{array}{l} P(X=x) & \quad \text{si $x$ est dans } R_X\\ 0 & \quad \text{sinon} \end{array} \right. \end {equation}

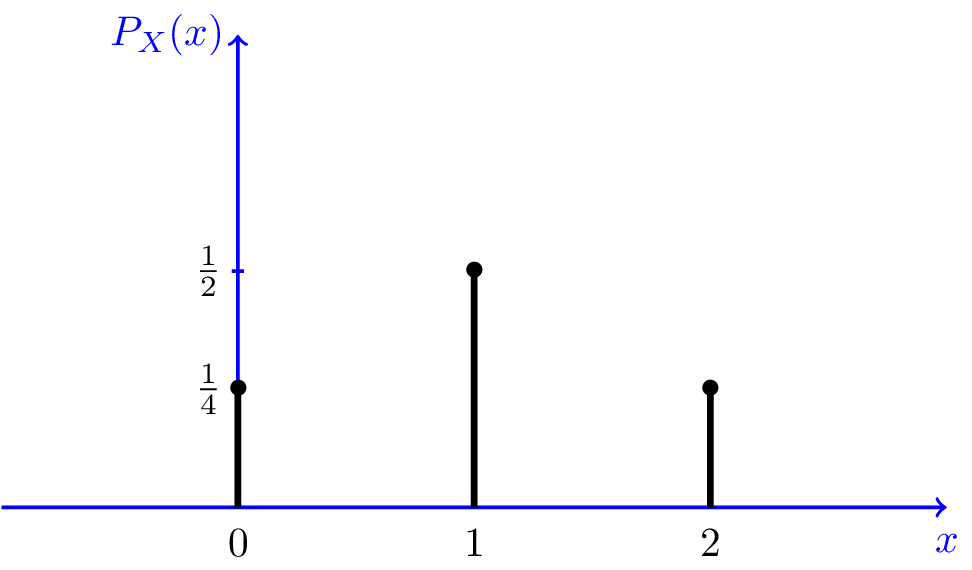
pour mieux visualiser le PMF, nous pouvons le tracer. Figure 3.,1 montre le PMF de la variable aléatoire ci-dessus X X$. Comme nous le voyons, la variable aléatoire peut prendre trois valeurs de $0,1$ et $2$. La figure indique également clairement que l’événement X X=1.est deux fois plus probable que les deux autres valeurs possibles. Le Chiffre peut être interprété de la manière suivante: Si l’on répète l’expérience aléatoire (en jetant une pièce de monnaie deux fois), un grand nombre de fois, puis environ la moitié du temps, nous observons $X=1$, environ un quart du temps, nous observons $X=0$, et environ un quart de fois nous observons $X=2$.

pour les variables aléatoires discrètes, la PMF est également appelée distribution de probabilité. Ainsi, lorsqu’on lui demande de trouver la distribution de probabilité d’une variable aléatoire discrète X X$, nous pouvons le faire en trouvant son PMF. La fonction de distribution de phrase est généralement réservée exclusivement à la fonction de distribution cumulative CDF (telle que définie plus loin dans le livre). Le mot distribution, d’autre part, dans ce livre est utilisé dans un sens plus large et pourrait se référer à PMF, fonction de densité de probabilité (PDF), ou CDF.,

Exemple

j’ai un injuste pièce pour laquelle $P(H)=p$, où $0

Considérons une variable aléatoire discrète X $$ avec la Gamme de$(X)=R_X$. Notez que par définition, le PMF est une mesure de probabilité, il satisfait donc toutes les propriétés d’une mesure de probabilité. En particulier, nous avons

• $0\leq P_X(x) \leq 1$ pour tout $x$, et
• $\sum_{x \in R_X} P_X(x)=1$.

notez également que pour tout ensemble r a \subset R_X$, nous pouvons trouver la probabilité que $X \ in A using en utilisant le PMF P P(X \in a)=\sum_{x \in A} P_X(x).,$$

Exemple

Pour la variable aléatoire $Y$ dans l’Exemple 3.4,

1. Vérifiez que $\sum_{y \in R_Y} P_Y(y)=1$.
2. Si $p=\frac{1}{2}$, trouvez $P(2\leq Y