Partie I
le développement du calcul
L’histoire a une façon de concentrer le crédit pour toute invention ou découverte sur un ou deux individus en un temps et en un lieu. La vérité n’est pas aussi soignée. Lorsque nous donnons l’impression que Newton et Leibniz ont créé le calcul à partir de tissu entier, nous rendons un mauvais service à nos étudiants. Newton et Leibniz étaient brillants, mais même eux n’étaient pas capables d’inventer ou de découvrir le calcul.,
le corps des mathématiques que nous connaissons sous le nom de calcul s’est développé au cours de plusieurs siècles dans de nombreuses régions du monde, non seulement en Europe occidentale, mais aussi en Grèce antique, au Moyen-Orient, en Inde, en Chine et au Japon. Newton et Leibniz se sont appuyés sur un vaste corpus de connaissances sur des sujets de calcul différentiel et intégral. Le sujet continuerait d’évoluer et de se développer longtemps après leur mort. Ce qui marque Newton et Leibniz, c’est qu’ils ont été les premiers à énoncer, comprendre et utiliser efficacement le théorème fondamental du calcul., Aucune personne n’a poussé notre compréhension du calcul aussi loin ou aussi vite. Mais les problèmes que nous étudions en calcul—Aires et volumes, vitesses associées, position/vitesse/accélération, séries infinies, équations différentielles—avaient été résolus avant la naissance de Newton ou de Leibniz.
il a fallu environ 1250 ans pour passer de l’intégrale d’un quadratique à celle d’un polynôme du quatrième degré. Mais la prise de conscience de cette lutte peut être un rappel utile pour nous. Les grands résultats de balayage qui résolvent si facilement tant de problèmes (l’intégration d’un polynôme étant un excellent exemple) cachent une longue lutte conceptuelle., Lorsque nous sautons trop vite vers l’algorithme magique et que nous ne reconnaissons pas les efforts qui ont été déployés pour sa création, nous risquons de traîner nos étudiants au-delà de cette compréhension conceptuelle.
Cet article explore l’histoire du calcul avant Newton et Leibniz: les personnes, les problèmes et les lieux qui font partie de la riche histoire du calcul.
trouver le Volume D’un Parabaloïde
Abu Ali Al-Hasan ibn al-Haytham (également connu sous la forme latinisée de son nom: Alhazen) était l’un des grands mathématiciens Arabes. Il est né à Bassora, en Perse, maintenant dans le Sud-Est de l’Irak., Quelque temps après 996, Il s’installe au Caire, en Égypte, où il s’associe à L’Université D’Al-Azhar, fondée en 970. Il a écrit plus de 90 livres, et est le plus célèbre pour son travail en astronomie et en optique. Son intérêt pour les mathématiques s’étendait sur l’algèbre, la géométrie et la théorie des nombres. Je me concentre sur lui parce qu’il est la première personne que je connais à avoir intégré un polynôme du quatrième degré.
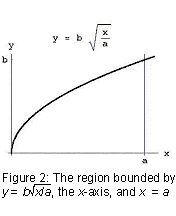
bien sûr, il ne l’a pas exprimé tout à fait de cette façon. Vers 250 av.,, Archimède a écrit sur les Conoïdes et les sphéroïdes, un livre qui, entre autres choses, a démontré comment trouver le volume d’un parabaloïde, le solide de révolution que vous obtenez lorsque vous faites pivoter une parabole autour de son axe (voir Figure 1)., En particulier, si a et b sont des constantes positives et que l’on prend la région délimitée ci-dessus par le graphe de la parabole ci-dessous par l’axe x, et à droite par x = a (voir Figure 2), et que l’on fait pivoter cette région autour de l’axe x, on obtient le solide de révolution dont le volume est
En d’autres termes, le volume est exactement la moitié de celui du cylindre que l’on obtient si l’on fait pivoter le rectangle de longueur a et de hauteur B autour du X-axe.
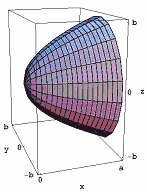
Figure 1: Le parabaloïde.

la Figure 1: La parabaloid.,

la partie La plus difficile de ce calcul, quelque chose qu’il a pris un mathématicien d’Archimède stature à réaliser, c’est que le problème de trouver le volume d’un parabaloid peut être réduite à celle de trouver l’aire sous une ligne droite (l’intégrale de x à partir de 0).,
dans le monde arabe du Xe siècle, Archimède sur les Conoïdes et les sphéroïdes était inconnu, mais Thabit ibn Qurra du Sud de la Turquie et Abu Sahl al-Kuhi du Nord de L’Iran avaient découvert leurs propres preuves du volume d’un parabaloïde. Ibn Al-Haytham a lu leur travail et s’est posé la question: et si nous tournions cette région autour de la ligne x = a au lieu de l’axe des x?
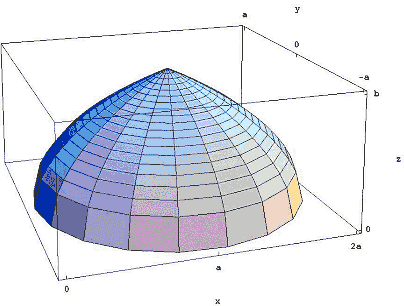
Figure 3: rotation de la région autour de la ligne x = a.
le résultat est le dôme très islamique illustré à la Figure 3., Ibn Al-Haytham a montré que son volume est 8 / 15e du volume du cylindre que vous obtenez lorsque vous faites pivoter le rectangle de longueur a et de hauteur b autour de x = a. Dans la notation du calcul moderne, le calcul de ce volume devient
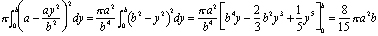
mais ibn Al-Haytham a vécu près de 700 ans avant que les formules pour les intégrales soient connues. Il a trouvé le volume en empilant des disques. Si nous découpons le dôme en disques nv, chacun d’épaisseur b / n, alors le disk Disque du bas a un rayon A – ai2/n2 et un volume (b/n) p (A – ai2/n2)2 (voir Figure 4)., Le volume total de cette pile de disques est
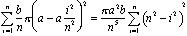
Il ne reste plus qu’à trouver une formule—en termes de n—pour la sommation. Nous voyons alors ce qui se passe lorsque n approche de l’infini. Nous étendons le terme et sortir de la constante des puissances de n:
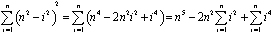
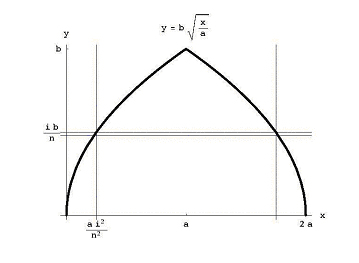
Figure 4: coupe horizontale à travers le dôme.
pour ibn Al-Haytham comme pour les mathématiciens du Moyen-Orient, de l’Asie du Sud et de l’Asie de l’est, le problème du calcul des aires et des volumes se résumait au problème de la recherche de sommes de puissances d’entiers consécutifs., Ibn Al-Haytham était l’un des nombreux mathématiciens dans de nombreux endroits différents qui ont réussi à résoudre ce problème. Il a montré que:
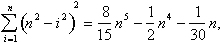
Le volume de la coupole est:
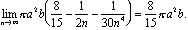
Comment pouvait-il trouver cette somme? Cette histoire s’étend sur plus de deux mille ans et trois continents.
partie II
Archimède et sommes de carrés
aucune description du calcul avant Newton et Leibniz ne pourrait être complète sans un compte rendu des contributions D’Archimède, Le Sicilien grec qui est né vers 287 avant J.-C. et est mort en 212 avant J.-C., pendant le siège romain de Syracuse. Nous examinerons l’un des nombreux problèmes de calcul qu’il a étudiés.
Il est courant de créditer Archimède des premiers agitations du calcul intégral. Parmi les problèmes qu’il a abordés et résolus figurent la recherche de zones sous les paraboles et à l’intérieur des spirales, et la recherche du volume de la sphère, des segments sphériques et du parabaloïde (le solide de révolution obtenu en faisant tourner une parabole autour de son axe). Il a également montré comment calculer la pente d’une droite tangente à une spirale, la première lueur du calcul différentiel.,
la beauté du calcul tel que nous le connaissons maintenant vient de sa simplicité. Le théorème fondamental du calcul nous permet de résoudre des problèmes très difficiles en appliquant des procédures de calcul simples justifiées par le théorème fondamental. Archimède ne les avait pas, il a donc dû s’appuyer sur des principes de base et, avec beaucoup d’ingéniosité, trouver des solutions intelligentes.
Archimède a trouvé des volumes du parabaloïde et d’autres solides en utilisant un argument d’équilibrage dans lequel il a comparé les moments de différents solides., Il a calculé l’aire sous la parabole pas par la méthode habituelle de l’approximation par une somme de carrés, mais en utilisant une méthode géométrique d’observation qui lui a permis de réduire le problème de trouver la somme d’une série géométrique. C’est l’une des nombreuses utilisations importantes des séries géométriques qui ont contribué au développement du calcul.
le problème sur lequel je veux me concentrer est celui de trouver la zone à l’intérieur d’une spirale. En coordonnées polaires, la spirale D’Archimède (voir Figure 5) est r = kq pour une constante K., En coordonnées rectangulaires, c’est la courbe d’équations paramétriques: x(t) = k · t · cos t, y(t) = k · t · sin t, t >= 0.
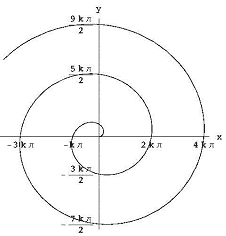
Figure 5: la spirale D’Archimède
Archimède a utilisé ce qui est devenu connu comme la « méthode de l’épuisement. »L’idée est d’approximer la surface en utilisant des pièces de plus en plus petites dont la surface peut être trouvée exactement, puis de prouver qu’une valeur particulière est la réponse en montrant que tout ce qui est plus petit est trop petit et tout ce qui est plus grand est trop grand.,
Archimède attribue cette méthode à Eudoxe de Cnide (408-355 av. j.-c.) Qui a prouvé que le volume d’une pyramide ou d’un cône correspond au tiers de la surface de la base multipliée par la hauteur. Alors Qu’Eudoxe a trouvé la première preuve, ce résultat est encore plus ancien: il a été trouvé par Démocrite (C. 465-375 B. C.). La formule du volume d’une pyramide a également été découverte dans l’Inde ancienne, et nous en avons la trace dans le livre Chinois Chiu Chang Suan Ching (neuf chapitres sur l’Art mathématique) qui peut avoir été écrit dès 150 avant JC.,
avant même que quiconque puisse prouver cette formule, la trouver nécessitait de penser à la pyramide comme composée de fines tranches, dont trois ensembles pouvaient être reconfigurés pour former un bloc rectangulaire. Plus tard dans cet article, nous verrons comment cette géométrie mentale en trois dimensions a conduit Archimède à la formule dont il avait besoin pour trouver l’aire de la spirale.
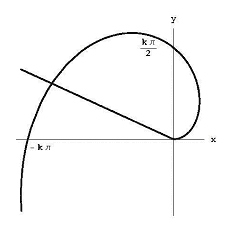
Figure 6: l’aire délimitée par la spirale D’Archimède et le rayon q = q1.,
en approchant l’aire de la spirale
pour trouver l’aire délimitée par la spirale et le rayon q = q1, comme le montre la Figure 6, Nous divisons l’angle entre les rayons en n petits angles de taille q1 / n. Si nous regardons le I morceau d’angle, la distance de la spirale de l’origine augmente de k(i – 1) q1/ n à ki q1/ N. cela signifie que notre aire se trouve à l’intérieur du secteur de rayon ki Q1/ n. notre aire comprend entièrement le secteur du cercle de rayon k(i – 1) Q1/ N.,
l’angle q1/ n représente q1 / 2 p N d’un cercle complet, donc l’aire de ce secteur est quelque part entre
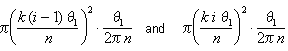
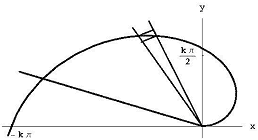
Figure 7: le secteur entre q = k(i – 1)q1/n et q=ki q1/n
lorsque nous simplifions, nous voyons que l’aire du segment segment se situe entre k2q 13 (I – 1)2/2N3 et k2q13 I2 /2N3. La surface totale se situe entre
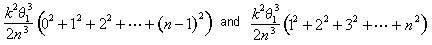
à ce stade, Archimède a dérivé une formule succincte pour la somme des premiers N – 1 carrés:
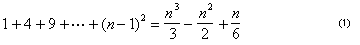 .,
.,
la zone sous la spirale se trouve quelque part entre
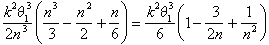
et
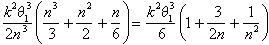
comme Archimède l’a maintenant soutenu, le seul nombre qui se trouve entre ces limites pour toutes les valeurs de n est k2 q13 /6.
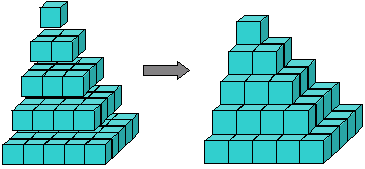
Figure 8: la pyramide des carrés
la formule de la somme des carrés
La formule de la somme des carrés n’était peut-être pas nouvelle pour Archimède, et il existe des preuves qu’elle pourrait avoir été découverte à peu près à la même époque en Inde. Nous savons qu’il a été redécouvert plusieurs fois., Les premières preuves, y compris la preuve D’Archimède, sont toutes géométriques.
Nous pouvons visualiser la somme des carrés comme une pyramide construite à partir de cubes (Figure 8). Archimède a montré comment prendre trois de ces pyramides, avec une triangulaire couche de blocs représentant 1+2···+(n – 1) et les assembler pour obtenir un bloc de cubes de n x n x (n – 1). En d’autres termes, il a montré que
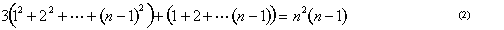 .
.
La formule 1+2+···+(n – 1)=n (n – 1)/2 est souvent attribuée à Gauss. L’histoire est qu’il l’a découvert lorsque son professeur lui a ordonné d’ajouter les entiers de 1 à 100., En fait, c’est une ancienne formule. On peut le trouver, par exemple, en Inde dans un manuscrit Jaïn de 300 av. j.-c.: Il aurait fait partie de L’enseignement mathématique D’Archimède. Il a une preuve géométrique très simple comme le montre la Figure 9.
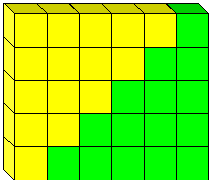
Figure 9: la preuve que 2 = n(n-1)
nous devons encore prouver l’équation (2), mais une fois que nous savons que c’est vrai, nous pouvons la combiner avec la formule pour la somme des premiers N – 1 entiers pour obtenir
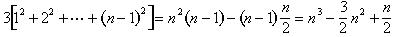 btenez l’équation (1).,
btenez l’équation (1).,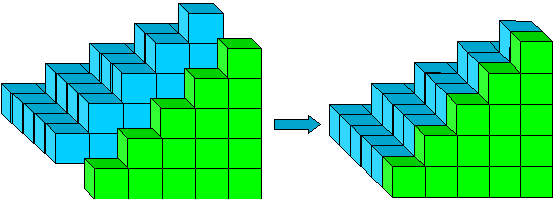
la Figure 10: 12+22+···+(n – 1)2 +1+2+···+(n – 1).
la Figure 11: 1· 2 + 2·3 + 3·4 +···+ (n-1)n = 2
L’équation algébrique qui correspond à cette image, c’est
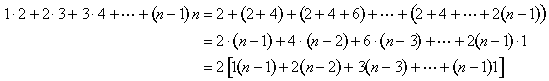
Ces pièces s’autour de la pyramide verte dans la Figure 8, de sorte que la pyramide inversée complète le n x n x (n – 1) bloc (Figure 12):
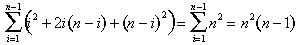
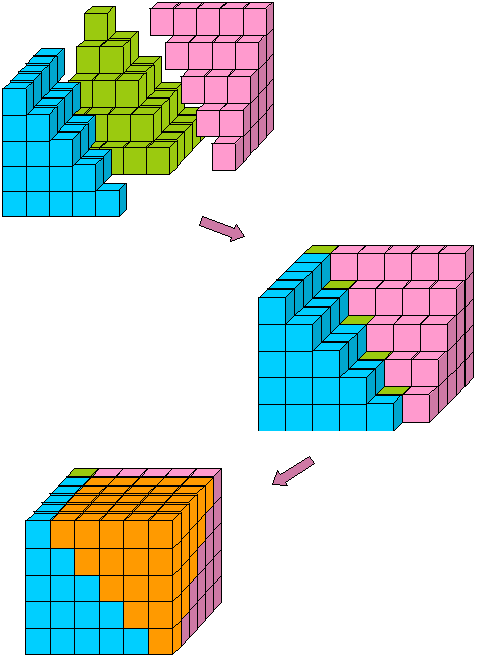
la Figure 12: Le n x n x (n – 1) bloc assemblé à partir de trois sommes de carrés et une somme d’entiers.,
sommes de Cubes
vous pourriez penser qu’après avoir vu l’utilité de la formule somme des carrés, Archimède aurait alors trouvé la formule pour la somme des cubes. Il a fallu plus de mille ans avant que quelqu’un le fasse. Le problème est que les sommes de carrés sont faciles à voir géométriquement. Les sommes de cubes peuvent être visualisées, mais l’objet que vous souhaitez les assembler pour former est en quatre dimensions. Mais comme nous le verrons dans la partie III, au moment où l’Europe était à son Moyen Âge, Les mathématiciens du Moyen-Orient, de l’Inde et de la Chine l’avaient tous fait.,
partie III
sommes de puissances
dans les deux premières parties de cet article, nous avons vu comment Archimède et ibn Al-Haytham ont utilisé des formules de sommes de puissances pour évaluer les aires et les volumes. À partir du 11ème siècle, les mathématiciens Arabes, chinois et Indiens ont commencé à découvrir des techniques qui leur permettraient de trouver la zone sous n’importe quel polynôme. Mais avant que quiconque puisse découvrir de telles formules, ils ont dû inventer des polynômes. Les polynômes quadratiques et cubiques existaient depuis plus de mille ans, mais exprimés en zones et en volumes., On ne savait même pas ce que signifierait un quatrième pouvoir. Les polynômes de degré supérieur ont émergé presque simultanément autour de l’an 1000 au Moyen-Orient, en Inde et en Chine.
deux contemporains du 11ème siècle, Abu Bakr al-Karaji à Bagdad et Jia Xian (un eunuque de cour chinoise) ont étudié des polynômes de haut degré, trouvé des méthodes d’extraction des racines et découvert ce que nous appelons aujourd’hui le triangle de Pascal. Al-Karaji a donné la première preuve connue de la formule pour la somme des cubes—également l’un des premiers exemples connus d’une preuve complète par induction.,
Somme des Cubes
Lorsque vous somme des cubes des entiers successifs, vous trouvez rapidement un schéma:
13 = 1, 13 + 2 3 = 9, 13 + 23 + 33 = 36, 13 + 23 + 33 +43 = 100, 13 +··· +53 = 225.
ce sont tous des carrés parfaits, et pas des carrés parfaits, mais
12, 32 = (1 + 2)2, 62 = (1 + 2 + 3)2, 102 = (1 + 2 + 3 + 4)2, 152 = (1 + ··· + 5)2.
la formule de la somme des cubes est facile à deviner:
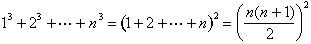
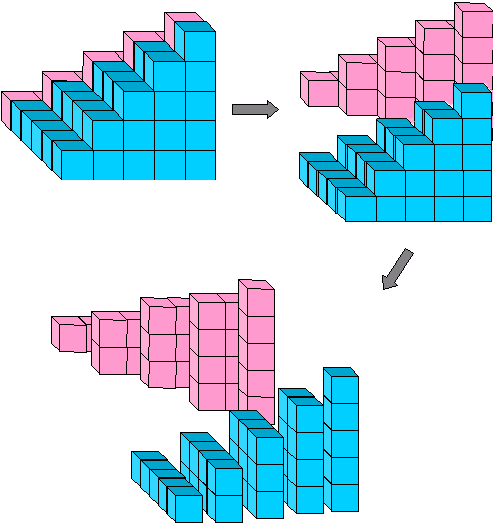
Aryabhata de Patna (dans ce qui est maintenant L’Inde) a découvert cette formule vers 500 de notre ère, et elle a peut-être été connue encore plus tôt., Il serait redécouvert par Abu al-Saqr Abd Al-Aziz ibn Uthman al-Qabisi au 10ème siècle à Bagdad et à nouveau au début du 14ème siècle en France par Levi ben Gerson. Nilakantha du Kerala (dans le sud-ouest de l’Inde) a donné une preuve visuelle en 1500 qui capture l’essence de la preuve d’al-Karaji.
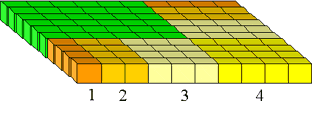
Figure 13: (1 + 2 + ··· + n)X(1 + 2+ ··· + n carrés).
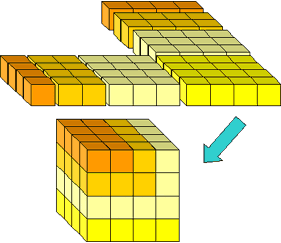
Figure 14: réorganiser les blocs restants en un cube.
Cette offre inductif étape de la preuve:
(1 + 2 + ··· + n)2 = n3 + (1 + 2 +··· + (n – 1))2.,
sommes des quatrièmes puissances
dans la première partie de cet article, nous avons vu qu’ibn Al-Haytham avait besoin de sommes des quatrièmes puissances pour trouver le volume du solide obtenu en faisant tourner une parabole autour d’une ligne perpendiculaire à l’axe de symétrie. Il a trouvé une telle formule. Bien que nous n’ayons aucune preuve qu’il ait poussé sa technique au-delà des quatrièmes puissances, son approche peut être utilisée pour trouver des formules pour des sommes d’entiers consécutifs à n’importe quelle puissance.
Al-Haytham a commencé par la formule de la somme des cubes. Il l’a utilisé pour bootstrap jusqu’à une formule pour les sommes de quatrième pouvoirs., regroupement de sorte que nous nous sommes consécutives de cubes:
(13 + 23 + ··· + (k – 1)3 + k3 )(k + 1)
= (14 + 24 + ··· + (k – 1)4) + k4 ) + 13 + (13 + 23) + (13 + 23 + 33) + ···
+ (13 + 23 + ··· + (k – 1)3 ) + (13 + 23 + ··· + k3)
Nous allons maintenant utiliser la formule pour la somme des cubes:
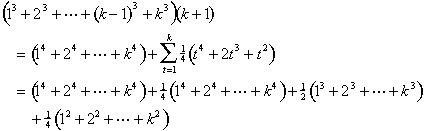
– Nous regrouper les termes semblables et utiliser les formules pour la somme de cubes et carrés de une fois de plus:
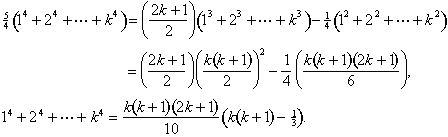
La même idée de travailler à trouver une formule pour la somme de cinquième pouvoirs en termes de la somme de la quatrième pouvoirs, et ainsi de suite.,
puissances supérieures
à Bagdad au XIIe siècle, puis indépendamment en Inde et en Chine au XIVe siècle, les mathématiciens ont découvert et exploité une propriété remarquable du triangle de Pascal. En commençant par le bord, descendez toute DIAGONALE qui se dirige vers le sud-ouest, en ajoutant les entrées. Où que vous vous arrêtiez, la somme de ces nombres est le nombre suivant au sud-est:
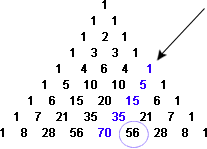
Figure 15: la somme des Termes sur une diagonale sud-ouest (1+5+15+35) est égal au terme suivant au sud-est (56).
Nous pouvons exprimer cela en termes de polynômes., Nous définissons un polynôme de degré n:
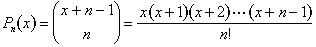
Cette propriété de diagonale sommes implique que pour les entiers positifs n et k, nous avons toujours
Pn(1) + Pn(2) + ··· + Pn(k) = Pn + 1(k).
x4 = 24P4(x) – 36p3(x) + 14p2 (x) – P1(x).
il s’ensuit que
14 + 24 + ··· + k4 = 24P5 ( k) – 36p4(k) + 14p3(k) – P2(k).
cette relation fondamentale pour les coefficients binomiaux est apparue pour la première fois dans Al-Bahir fi’l Hisab (brillant Traité de calcul) écrit par al-Samaw’al en 1144 dans L’Irak actuel., Il peut également être trouvé dans Siyuan Yujian écrit par Zhu Shijie en 1303 en Chine, et le Ganita Kaumudi écrit par Narayana Pandita en 1356 en Inde.
Remarquable que cette méthode est, il n’est pas la meilleure façon de trouver des formules pour les sommes de puissances. Cela a été découvert par le mathématicien suisse Jacob Bernoulli au début du 18ème siècle. Depuis deux mille ans, les mathématiciens utilisent des formules de sommes de puissances pour calculer des aires. Bernoulli a utilisé le calcul intégral pour trouver des dérivations simples de la somme des formules de puissances. Mais c’est une autre histoire.,
ressources
Calinger, Ronald. Une histoire contextuelle des mathématiques: à Euler. Upper Saddle River, New Jersey: Prentice Hall, 1999.
Dick, Thomas P., et Charles M. Patton. Calcul. Boston, Mass.: PWS Édition, 1995.
Dijksterhuis, E. J. Archimède. Traduit par C. Dikshoorn. 1938. Princeton, N. J., Princeton University Press, 1987.
Heath, Thomas. Une histoire des mathématiques grecques. 2 vols. Oxford: Oxford University Press, 1921. Réimpression: Douvres, 1981.
Katz, Victor J. Une histoire des mathématiques: une Introduction. 2ème édition. New York: Harper Collins, 1998.,
—. « Idées de calcul dans L’Islam et L’Inde. »Les Mathématiques Magazine 68-3 (1995): 163-174.
Martzloff, Jean-Claude. Une histoire des mathématiques chinoises. Traduit par Stephen S. Wilson. New York: Springer-Verlag, 1998.
Saraswathi, T. A. « Le développement des séries mathématiques en Inde après Bhaskara II. » Bulletin de L’Institut National des Sciences 21 (1963): 320-343.
Stein, Sherman. Archimède: Qu’A-T-Il Fait À Part Pleurer Eureka? Il s’agit de la première édition de la série télévisée américaine « The Mathematical Association of America », publiée en 1999.