Parte I
el desarrollo del cálculo
La historia tiene una forma de enfocar el crédito para cualquier invención o descubrimiento en uno o dos individuos en un tiempo y lugar. La verdad no es tan clara. Cuando damos la impresión de que Newton y Leibniz crearon el cálculo de toda la tela, hacemos un flaco favor a nuestros estudiantes. Newton y Leibniz eran brillantes, pero ni siquiera ellos eran capaces de inventar o descubrir el cálculo.,
el cuerpo de las matemáticas que conocemos como cálculo se desarrolló durante muchos siglos en muchas partes diferentes del mundo, no solo en Europa occidental, sino también en la antigua Grecia, Oriente Medio, India, China y Japón. Newton y Leibniz se basaron en un vasto cuerpo de conocimientos sobre temas de cálculo diferencial e integral. El tema seguiría evolucionando y desarrollándose mucho después de su muerte. Lo que marca a Newton y Leibniz es que fueron los primeros en afirmar, entender y utilizar eficazmente el Teorema Fundamental del cálculo., No hay dos personas que hayan movido nuestra comprensión del cálculo tan lejos o tan rápido. Pero los problemas que estudiamos en el cálculo-áreas y volúmenes, tasas relacionadas, posición / velocidad / aceleración, series infinitas, ecuaciones diferenciales-se habían resuelto antes de que nacieran Newton o Leibniz.
tomó unos 1.250 años para pasar de la integral de un cuadrático a la de un polinomio de cuarto grado. Pero la conciencia de esta lucha puede ser un recordatorio útil para nosotros. Los grandes resultados que resuelven tantos problemas tan fácilmente (la integración de un polinomio es un ejemplo principal) ocultan una larga lucha conceptual., Cuando saltamos demasiado rápido al algoritmo mágico y no reconocemos el esfuerzo que se realizó en su creación, corremos el riesgo de arrastrar a nuestros estudiantes más allá de esa comprensión conceptual.
Este artículo explora la historia del cálculo antes de Newton y Leibniz: las personas, los problemas y los lugares que forman parte de la rica historia del cálculo.
encontrar el volumen de un Parabaloide
Abu Ali Al-Hasan ibn al-Haytham (también conocido por la forma latinizada de su nombre: Alhazen) fue uno de los grandes matemáticos Árabes. Nació en Basora, Persia, ahora en el sureste de Irak., En algún momento después de 996, se trasladó a El Cairo, Egipto, donde se asoció con la Universidad de Al-Azhar, fundada en 970. Escribió más de 90 libros, y es más famoso por su trabajo en astronomía y óptica. Su interés en las matemáticas se extendía sobre álgebra, geometría y teoría de números. Me enfoco en él porque es la primera persona que conozco que ha integrado un polinomio de cuarto grado.
Por supuesto, él no lo expresó de esa manera. Alrededor de 250 A. C., Arquímedes escribió sobre Conoides y esferoides, un libro que, entre otras cosas, demostró cómo encontrar el volumen de un parabaloide, el sólido de revolución que se obtiene cuando se gira una parábola alrededor de su eje (ver Figura 1)., En particular, si a y b son constantes positivas y tomamos la región limitada arriba por el gráfico de la parábola abajo por el eje x, y a la derecha por x = a ( ver Figura 2), y giramos esta región alrededor del eje x, obtenemos el sólido de revolución cuyo volumen es
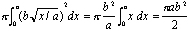
En otras palabras, el volumen es exactamente la mitad que el del cilindro que obtienes si rotas el rectángulo de longitud A y altura b alrededor del eje X.
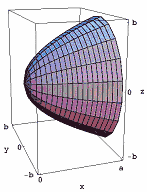
Figura 1: el parabaloide.

Figura 1: el parabaloide.,
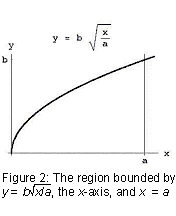

La parte más difícil de este cálculo, algo que tomó un matemático de Arquímedes estatura darse cuenta de que, es que el problema de encontrar el volumen de un parabaloid puede ser reducida a la de hallar el área bajo una línea recta (la integral de x desde 0 a a).,
en el mundo árabe del siglo X, Arquímedes sobre Conoides y esferoides era desconocido, pero Thabit ibn Qurra del Sur de Turquía y Abu Sahl al-Kuhi del norte de Irán habían descubierto sus propias pruebas del volumen de un parabaloide. Ibn al – Haytham leyó su trabajo y se hizo la pregunta: ¿Qué pasa si giramos esta región alrededor de la línea x = a en lugar del eje x?
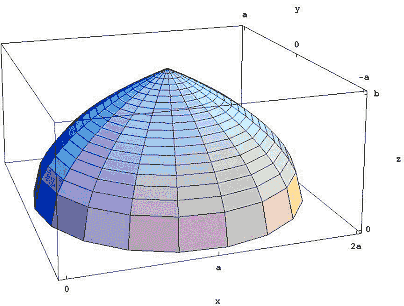
Figura 3: girando la región alrededor de la línea x = A.
el resultado es la cúpula de aspecto muy islámico que se muestra en la Figura 3., Ibn al – Haytham mostró que su volumen es 8/15 del volumen del cilindro que se obtiene al rotar el rectángulo de longitud a y altura B alrededor de x = A.en la notación del cálculo moderno, el cálculo de este volumen se convierte en
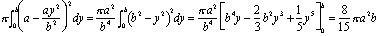
pero ibn al-Haytham vivió casi 700 años antes de que se conocieran las fórmulas para integrales. Encontró el volumen apilando discos. Si cortamos la cúpula en discos nv, cada uno de espesor b / n, entonces el disco ith de la parte inferior tiene radio a-ai2 / n2 y volumen (b/n) p (a – ai2/n2)2 (ver Figura 4)., El volumen total de esta pila de discos
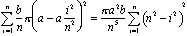
Todo lo que queda es encontrar una fórmula en términos de n—para la suma. Luego vemos lo que sucede cuando n se acerca al infinito. Expandimos el sumando y extraemos las potencias constantes de n:
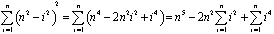
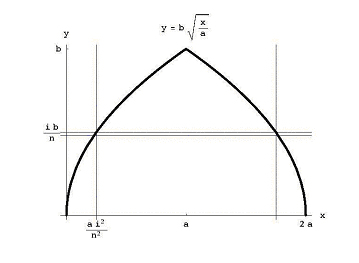
Figura 4: El Corte horizontal a través del domo.
para ibn al-Haytham como para los matemáticos en el Medio Oriente, Asia del Sur y Asia oriental, el problema de calcular áreas y volúmenes se redujo al problema de encontrar sumas de potencias de enteros consecutivos., Ibn al-Haytham fue uno de los muchos matemáticos en muchos lugares diferentes que tuvo éxito en la solución de este problema. Él mostró que:
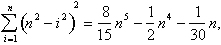
El volumen de la cúpula es de:
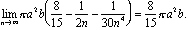
¿Cómo encontrar este balance? Esa historia abarca más de dos mil años y tres continentes.
Parte II
Arquímedes y sumas de cuadrados
ninguna Descripción del cálculo antes de Newton y Leibniz podría estar completa sin una cuenta de las contribuciones de Arquímedes, el siciliano griego que nació alrededor de 287 AC y murió en 212 AC., durante el asedio romano de Siracusa. Vamos a ver uno de los muchos problemas de cálculo que estudió.
Es común atribuir a Arquímedes los primeros movimientos del cálculo integral. Entre los problemas que abordó y resolvió están encontrar áreas bajo parábolas y espirales interiores, y encontrar el volumen de la esfera, los segmentos esféricos y el parabaloide (el sólido de revolución obtenido girando una parábola alrededor de su eje). También mostró cómo calcular la pendiente de una recta tangente a una espiral, el primer destello de cálculo diferencial.,
la belleza del cálculo como lo conocemos ahora proviene de su simplicidad. El Teorema Fundamental del cálculo nos permite resolver problemas muy difíciles mediante la aplicación de procedimientos de cálculo simples que están justificados por el Teorema Fundamental. Arquímedes no tenía estos, por lo que tuvo que confiar en los principios básicos y, con una gran cantidad de ingenio, llegar a soluciones inteligentes.
Arquímedes encontró volúmenes del parabaloide y otros sólidos usando un argumento de equilibrio en el que comparó los momentos de diferentes sólidos., Calculó el área bajo una parábola no por el método habitual de aproximación por una suma de cuadrados, pero mediante el uso de una observación geométrica que le permitió reducir el problema para encontrar la suma de una serie geométrica. Este es uno de varios usos importantes de las series geométricas que contribuyeron al desarrollo del cálculo.
el problema en el que quiero centrarme es el de encontrar el área dentro de una espiral. En coordenadas polares, la espiral de Arquímedes (ver Figura 5) es r = kq para alguna constante k., En coordenadas rectangulares, es la curva con ecuaciones paramétricas: x(t) = k · t · cos t, y(t) = k · t · sen t, t >= 0.
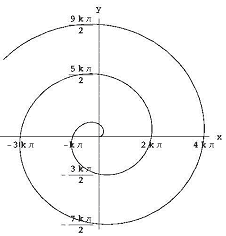
Figura 5: La espiral de Arquímedes
Arquímedes empleó lo que ha llegado a conocerse como el «método de agotamiento».»La idea es aproximar el área usando piezas cada vez más pequeñas cuyo área se puede encontrar exactamente, y luego probar que un valor particular es la respuesta al mostrar que cualquier cosa más pequeña es demasiado pequeña y cualquier cosa más grande es demasiado grande.,
Arquímedes atribuye este método a Eudoxo de Cnido (408-355 A.C.) quien demostró que el volumen de cualquier pirámide o cono es un tercio del área de la base multiplicada por la altura. Mientras que Eudoxo encontró la primera prueba, este resultado es aún más antiguo: fue encontrado por Demócrito (C. 465-375 B. C.). La fórmula para el volumen de una pirámide también fue descubierta en la India antigua, y tenemos registro de ella en el Libro Chino Chiu Chang Suan Ching (nueve capítulos sobre el arte matemático) que puede haber sido escrito ya en 150 B. C.,
incluso antes de que alguien pudiera probar esta fórmula, para encontrarla era necesario pensar en la pirámide como si estuviera formada por finas rebanadas, tres conjuntos de las cuales podrían reconfigurarse para hacer un bloque rectangular. Más adelante en este artículo veremos cómo esta geometría tridimensional mental llevó a Arquímedes a la fórmula que necesitaba para encontrar el área de la espiral.
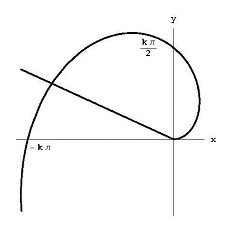
Figura 6: el área limitada por la espiral de Arquímedes y el rayo q = q1.,
aproximando el área de la espiral
para encontrar el área limitada por la espiral y el rayo q = q1, como se muestra en la Figura 6, dividimos el ángulo entre los rayos en n ángulos pequeños de tamaño q1 / n. Si miramos la i – ésima pieza de ángulo, la distancia de la espiral desde el origen aumenta de k(i – 1) q1/ N A ki q1/ n. esto significa que nuestra área se encuentra dentro del sector de radio ki q 1/ n. Nuestra área incluye enteramente el sector de la círculo de radio k(i-1) Q1/ n.,
el ángulo q1/ n representa q1 / 2 p n de un círculo completo, por lo que el área de este sector está en algún lugar entre
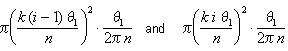
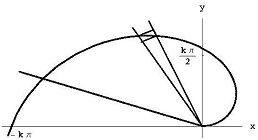
Figura 7: el sector entre q = k(i – 1)q1/n y q=ki q1/n
Cuando simplificamos estos límites, vemos que el área del segmento I se encuentra entre k2q 13 (I – 1)2/2N3 y k2q13 I2 /2N3. El área total se encuentra entre
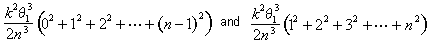
en este punto, Arquímedes derivó una fórmula sucinta para la suma de los primeros cuadrados n – 1:
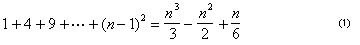 .,
.,
el área bajo la espiral se encuentra en algún lugar entre
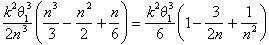
y
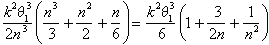
como Arquímedes argumentó ahora, el único número que se encuentra entre estos límites para todos los valores de n es k2 q13 /6.
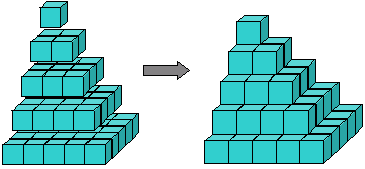
Figura 8: la pirámide de cuadrados
la fórmula para la suma de cuadrados
la fórmula para la suma de cuadrados puede no haber sido nueva para Arquímedes, y hay evidencia de que podría haber sido descubierta casi al mismo tiempo en la India. Sabemos que fue redescubierta muchas veces., Las primeras pruebas, incluyendo la prueba de Arquímedes, son todas geométricas.
podemos visualizar la suma de cuadrados como una pirámide construida a partir de cubos (Figura 8). Arquímedes mostró cómo tomar tres de estas pirámides junto con una capa triangular de bloques que representan 1+2···+ (n – 1) y encajarlos juntos para obtener un bloque de cubos n x N x (n – 1). En otras palabras, mostró que
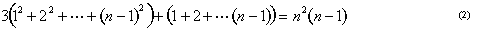 .
.
La fórmula 1+2+···+(n – 1)=n (n – 1)/2 se atribuye a menudo a Gauss. La historia es que lo descubrió cuando su maestro le ordenó agregar los números enteros del 1 al 100., De hecho, es una fórmula antigua. Se puede encontrar, por ejemplo, en la India en un manuscrito de Jain del 300 A. C.: habría sido parte de la instrucción matemática de Arquímedes. Tiene una prueba geométrica muy simple como se muestra en la Figura 9.
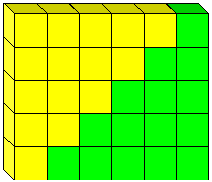
Figura 9: la prueba de que 2 = n(n-1)
todavía tenemos que probar la ecuación (2), pero una vez que sabemos que es verdadera, podemos combinarla con la fórmula para la suma de los primeros enteros n – 1 para obtener
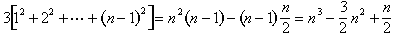
dividir ambos lados por 3, y obtener ecuación (1).,
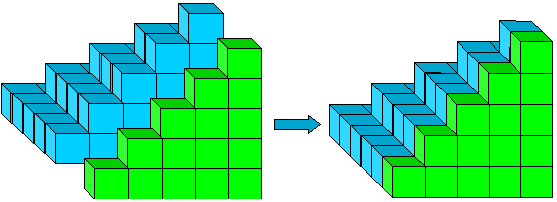
Figura 10: 12+22+···+(n – 1)2 +1+2+···+(n – 1).
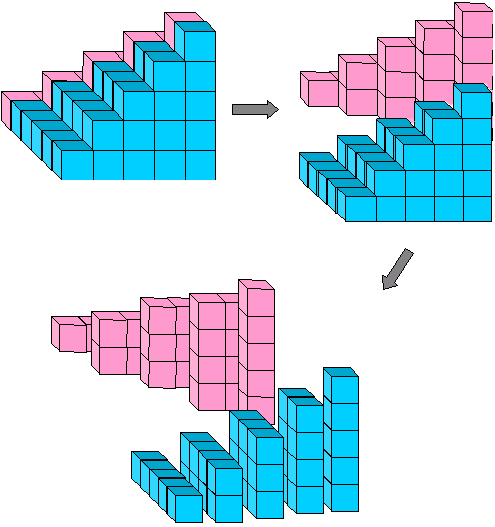
Figura 11: 1· 2 + 2·3 + 3·4 +···+ (n-1) n=2
la ecuación algebraica que corresponde a esta imagen es
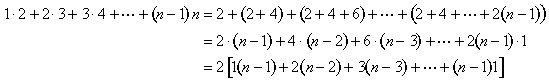
estas piezas encajan alrededor de la pirámide verde en la Figura 8 para que una pirámide invertida más complete el bloque n x n x (N – 1) (Figura 12):
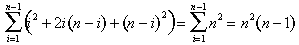
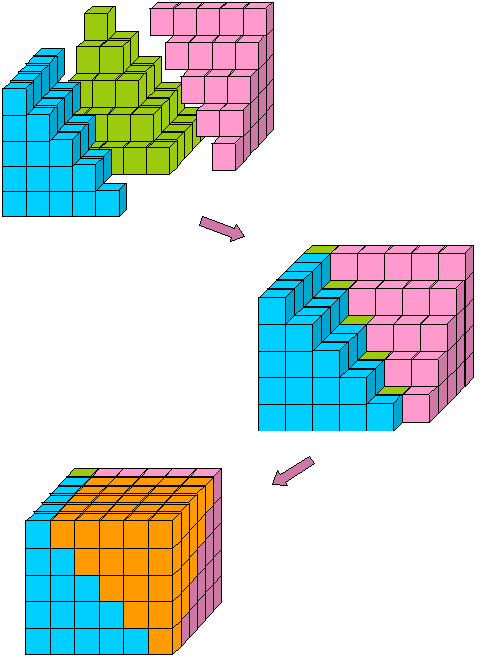
figura 12: el bloque n x n x (n – 1) ensamblado a partir de tres sumas de cuadrados y una suma de enteros.,
sumas de cubos
podrías pensar que habiendo visto lo útil que es la fórmula de la suma de cuadrados, Arquímedes habría encontrado la fórmula para la suma de cubos. Tomó más de mil años antes de que alguien lo hiciera. El problema es que las sumas de cuadrados son fáciles de ver geométricamente. Se pueden visualizar sumas de cubos, pero el objeto que desea juntar para formar es de cuatro dimensiones. Pero como veremos en la Parte III, en el momento en que Europa estaba en su edad media, los matemáticos en el Medio Oriente, India y China lo habían hecho.,
Parte III
sumas de poderes
en las dos primeras partes de este artículo, vimos cómo Arquímedes e ibn al-Haytham usaron fórmulas para sumas de poderes para evaluar áreas y volúmenes. A partir del siglo XI, los matemáticos árabes, chinos e indios comenzaron a descubrir técnicas que les permitirían encontrar el área bajo cualquier polinomio. Pero antes de que alguien pudiera descubrir tales fórmulas, tenían que inventar polinomios. Los polinomios cuadráticos y cúbicos habían existido durante más de mil años, pero expresados como áreas y volúmenes., Ni siquiera estaba claro lo que significaría una cuarta potencia. Polinomios de grado superior surgieron casi simultáneamente alrededor del año 1000 en el Medio Oriente, India y China.
dos contemporáneos del siglo XI, Abu Bakr Al-Karaji en Bagdad y Jia Xian (un eunuco de la Corte China) estudiaron polinomios de alto grado, encontraron métodos para extraer raíces y descubrieron lo que hoy llamamos el triángulo de Pascal. Al-Karaji dio la primera prueba conocida de la fórmula para la suma de cubos—también uno de los primeros ejemplos conocidos de una prueba completa por inducción.,
Sumas de Cubos
Cuando usted suma de los cubos de los sucesivos números enteros, encontrar rápidamente un patrón:
13 = 1, 13 + 2 3 = 9, 13 + 23 + 33 = 36, 13 + 23 + 33 +43 = 100, 13 +··· +53 = 225.
Estos son todos los cuadrados perfectos, y no cualquier cuadrados perfectos, pero
12, 32 = (1 + 2)2, 62 = (1 + 2 + 3)2, 102 = (1 + 2 + 3 + 4)2, 152 = (1 + ··· + 5)2.
la fórmula para la suma de cubos es fácil de adivinar:
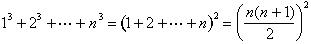
Aryabhata de Patna (en lo que ahora es India) descubrió esta fórmula alrededor del 500 E. C., y puede haber sido conocida incluso antes., Sería redescubierta por Abu Al-Saqr Abd Al-Aziz ibn Uthman al-Qabisi en Bagdad del siglo X y de nuevo a principios del siglo XIV en Francia por Levi ben Gerson. Nilakantha de Kerala (en el suroeste de la India) dio una prueba visual en 1500 que captura la esencia de la prueba de Al-Karaji.
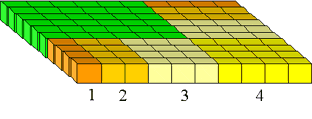
Figura 13: El (1 + 2 + ··· + n) X(1 + 2+ ··· + n) cuadrado.
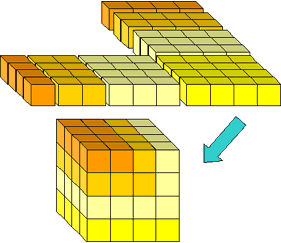
Figura 14: reordenando los bloques restantes en un cubo.
Esto proporciona el paso inductivo de la prueba:
(1 + 2 + ··· + n)2 = n3 + (1 + 2 +··· + (n – 1))2.,
sumas de cuartas potencias
en la Parte I de este artículo, vimos que ibn al-Haytham necesitaba sumas de cuartas potencias para encontrar el volumen del sólido obtenido girando una parábola alrededor de una recta perpendicular al eje de simetría. Encontró una fórmula. Si bien no tenemos evidencia de que empujó su técnica más allá de las cuartas potencias, su enfoque se puede utilizar para encontrar fórmulas para sumas de enteros consecutivos a cualquier potencia.
Al-Haytham comenzó con la fórmula para la suma de cubos. Lo usó para arrancar una fórmula para sumas de cuartos poderes., reagrupamiento de obtener sumas de cubos consecutivos:
(13 + 23 + ··· + (k – 1)3 + k3 )(k + 1)
= (14 + 24 + ··· + (k – 1)4) + k4 ) + 13 + (13 + 23) + (13 + 23 + 33) + ···
+ (13 + 23 + ··· + (k – 1)3 ) + (13 + 23 + ··· + k3)
ahora utilizamos la fórmula para la suma de cubos:
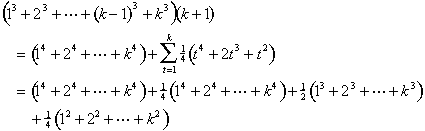
Nos consolidar términos similares y utilizar las fórmulas para las sumas de cubos y cuadrados, una vez más:
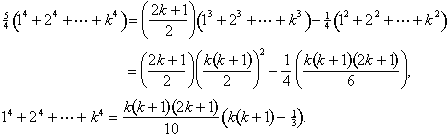
de La misma idea de trabajar para encontrar una fórmula para la suma de la quinta poderes en términos de la suma de la cuarta poderes, y así sucesivamente.,
poderes superiores
en Bagdad del siglo XII y luego de forma independiente en la India y China del siglo XIV, los matemáticos descubrieron y explotaron una propiedad notable del triángulo de Pascal. Comenzando en el borde, baje cualquier diagonal que se dirija al suroeste, agregando las entradas. Donde quiera que te detengas, la suma de estos números es el siguiente número al sureste:
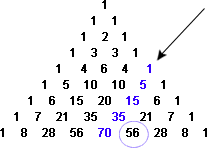
Figura 15: la suma de términos en una diagonal suroeste (1+5+15+35) es igual al siguiente término al sureste (56).
podemos expresar esto en términos de polinomios., Se define un polinomio de grado n:
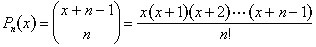
Esta propiedad de diagonal sumas implica que para los enteros positivos n y k, siempre tenemos
Pn(1) + Pn(2) + ··· + Pn(k) = Pn + 1(k).
x4 = 24P4 ( x) – 36p3(x) + 14p2 (x) – P1(x).
Se sigue que
14 + 24 + ··· + k4 = 24P5(k) – 36P4(k) + 14P3(k) – P2(k).
esta relación fundamental para los coeficientes binomiales apareció por primera vez en Al-Bahir fi’l Hisab (Tratado brillante sobre el cálculo) escrito por al-Samaw’al en 1144 en el actual Iraq., También se puede encontrar en Siyuan Yujian escrito por Zhu Shijie en 1303 en China, y el Ganita Kaumudi escrito por Narayana Pandita en 1356 en la India.
notable como este método es, no es la mejor manera de encontrar fórmulas para las sumas de poderes. Eso fue descubierto por el matemático suizo Jacob Bernoulli a principios del siglo 18. Durante dos mil años, los matemáticos habían estado utilizando fórmulas de sumas de poderes para calcular áreas. Bernoulli utilizó el cálculo integral para encontrar derivaciones simples de las fórmulas de la suma de potencias. Pero esa es otra historia.,
Resources
Calinger, Ronald. A Contextual History of Mathematics: to Euler (en inglés). Upper Saddle River, N. J.: Prentice Hall, 1999.
Dick, Thomas P., y Charles M. Patton. Calculo. Boston, Mass.: PWS Publishing, 1995.Dijksterhuis, E. J. Archimedes. Traducido por C. Dikshoorn. 1938. Princeton, N. J.: Princeton University Press, 1987.Heath, Thomas. A History of Greek Mathematics (en inglés). 2 vols. Oxford: Oxford University Press, 1921. Reprint: Dover, 1981.
Katz, Victor J. A History of Mathematics: An Introduction (en inglés). 2nd edition. New York: Harper Collins, 1998.,
– – -. «Ideas of Calculus in Islam and India.»Mathematics Magazine 68-3( 1995): 163-174.Martzloff, Jean-Claude. A History of Chinese Mathematics (en inglés). Traducido por Stephen S. Wilson. New York: Springer-Verlag, 1998.
Saraswathi, T. A. «The Development of Mathematical Series in India After Bhaskara II.» Bulletin of the National Institute of Sciences 21 (1963): 320-343.Stein, Sherman. Arquímedes: ¿Qué Hizo Además De Llorar Eureka? Washington, D. C.: The Mathematical Association of America, 1999.